-
- Downloads
updates
Showing
- Operationsverstaerker/README.md 1 addition, 1 deletionOperationsverstaerker/README.md
- Operationsverstaerker/doc/Hinweise-Grundschaltungen.md 23 additions, 15 deletionsOperationsverstaerker/doc/Hinweise-Grundschaltungen.md
- Operationsverstaerker/doc/Hinweise-Innenbeschaltung.md 26 additions, 34 deletionsOperationsverstaerker/doc/Hinweise-Innenbeschaltung.md
- Operationsverstaerker/doc/Hinweise-Komplexere-Schaltungen.md 10 additions, 10 deletionsOperationsverstaerker/doc/Hinweise-Komplexere-Schaltungen.md
- Operationsverstaerker/doc/Hinweise-OPV.md 22 additions, 22 deletionsOperationsverstaerker/doc/Hinweise-OPV.md
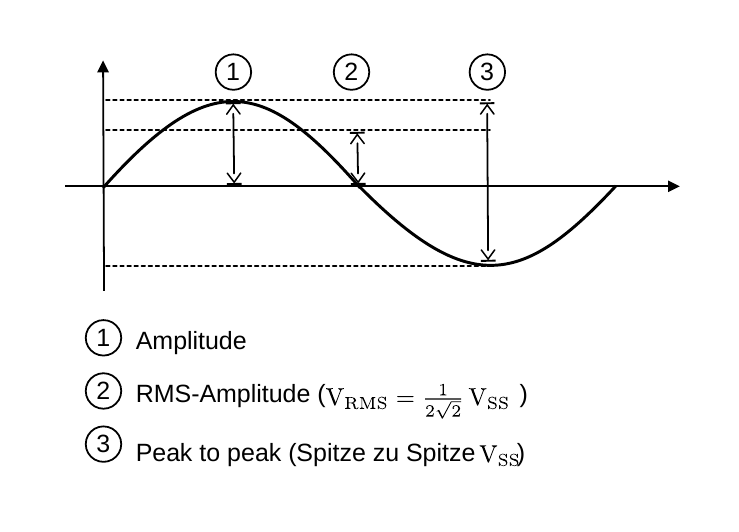
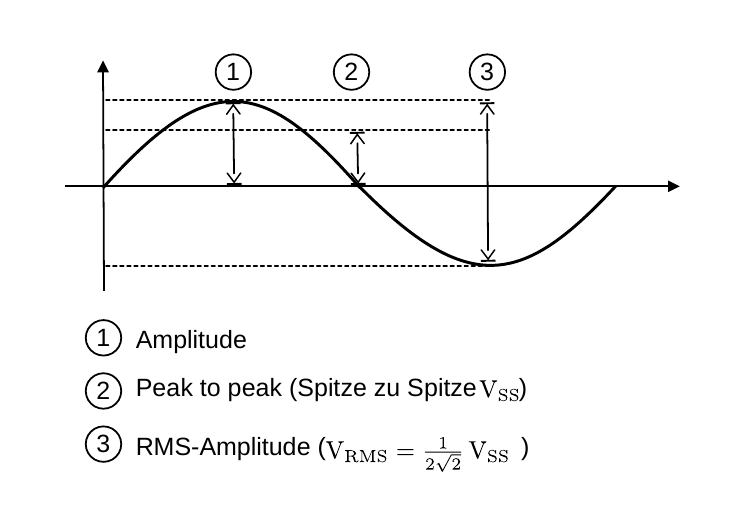
- Operationsverstaerker/figures/Amplitudenangaben.odg 0 additions, 0 deletionsOperationsverstaerker/figures/Amplitudenangaben.odg
- Operationsverstaerker/figures/Amplitudenangaben.png 0 additions, 0 deletionsOperationsverstaerker/figures/Amplitudenangaben.png
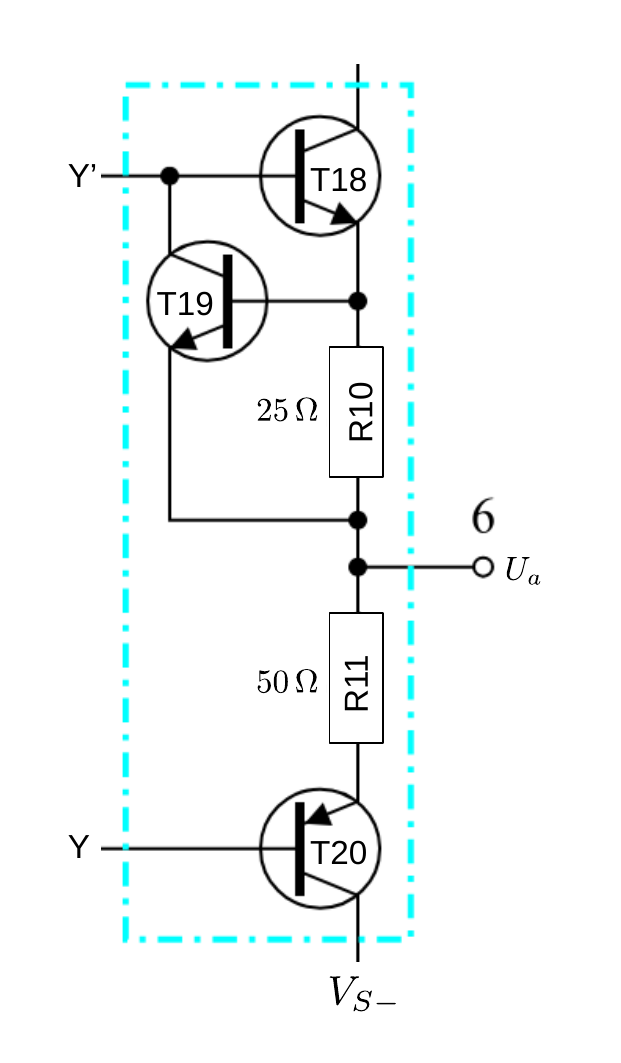
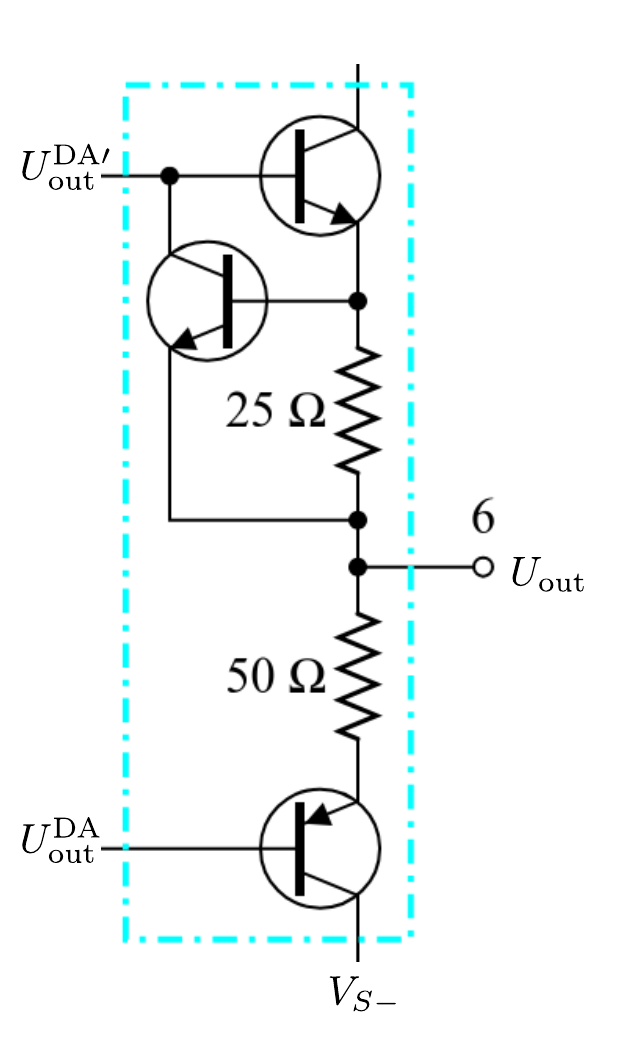
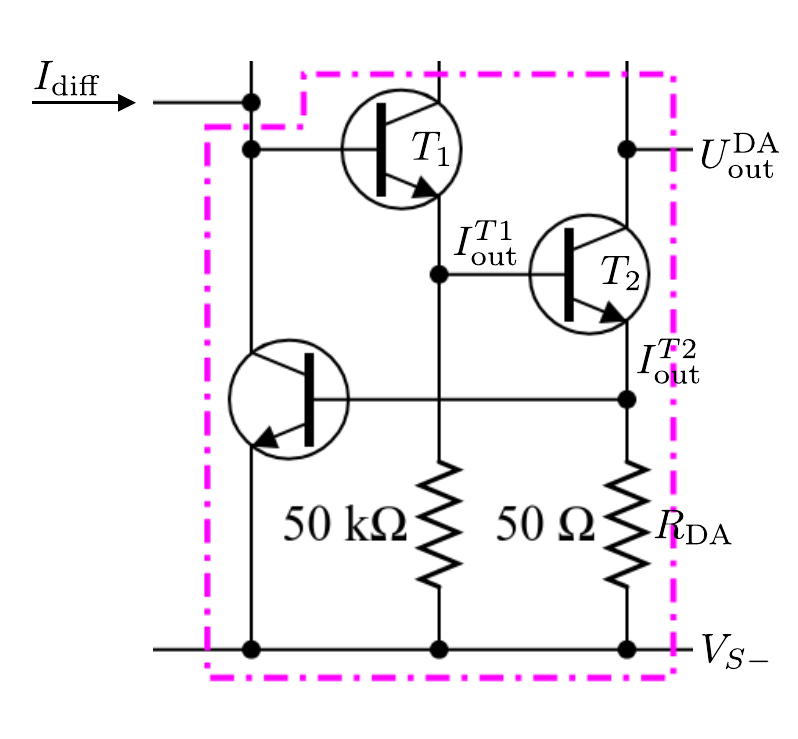
- Operationsverstaerker/figures/OPV_Ausgangsstufe.odg 0 additions, 0 deletionsOperationsverstaerker/figures/OPV_Ausgangsstufe.odg
- Operationsverstaerker/figures/OPV_Ausgangsstufe.png 0 additions, 0 deletionsOperationsverstaerker/figures/OPV_Ausgangsstufe.png
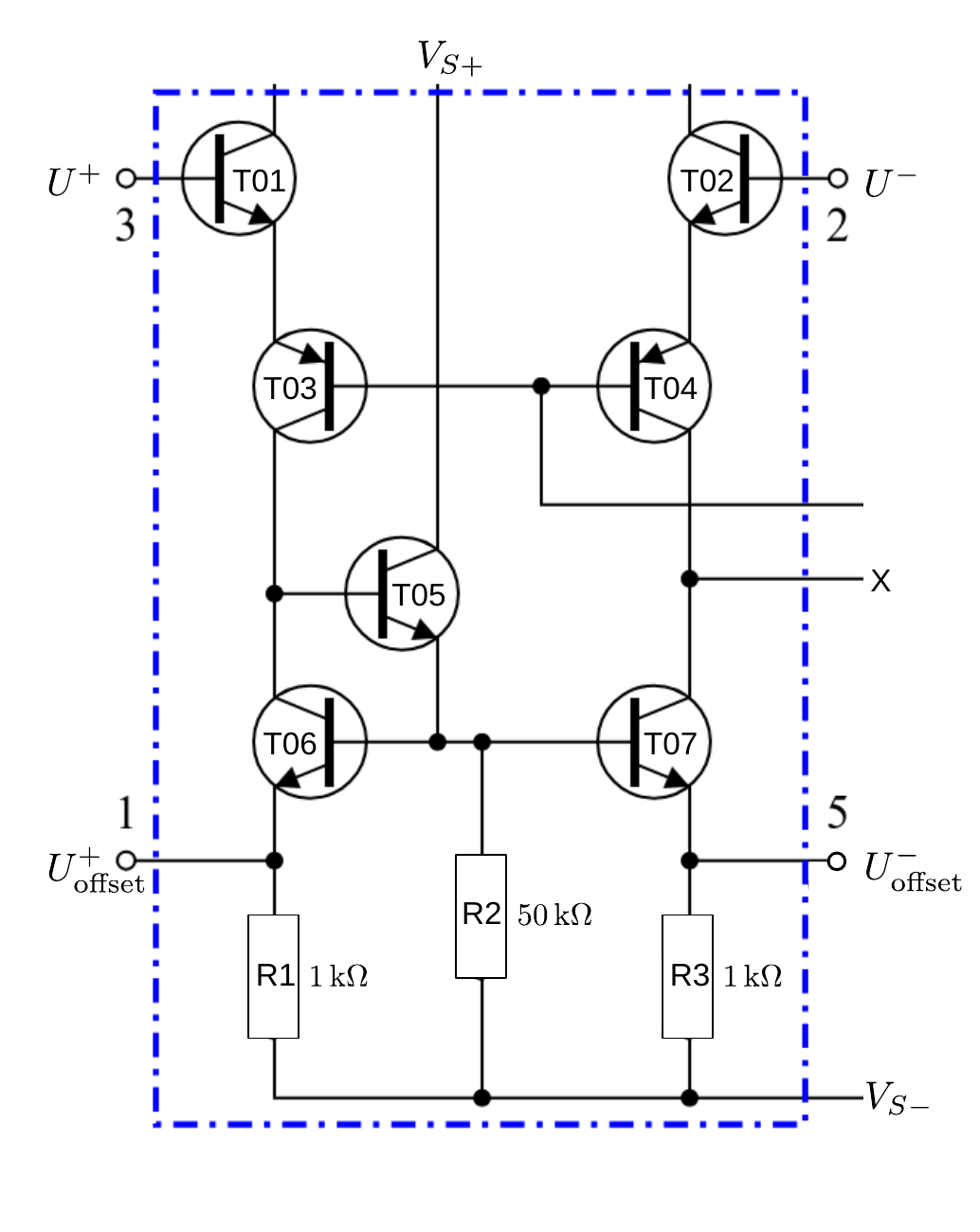
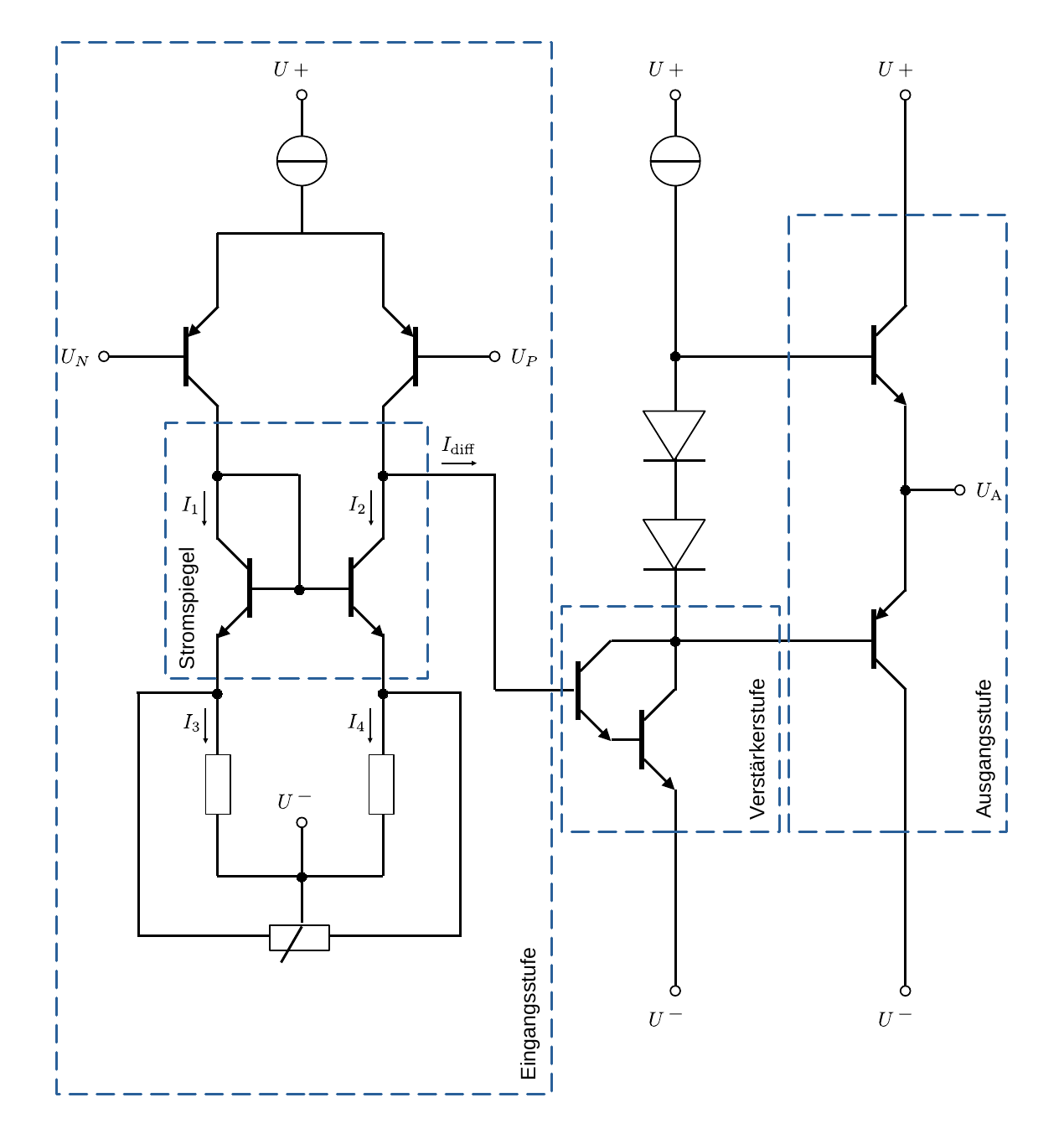
- Operationsverstaerker/figures/OPV_Eingangsstufe.odg 0 additions, 0 deletionsOperationsverstaerker/figures/OPV_Eingangsstufe.odg
- Operationsverstaerker/figures/OPV_Eingangsstufe.png 0 additions, 0 deletionsOperationsverstaerker/figures/OPV_Eingangsstufe.png
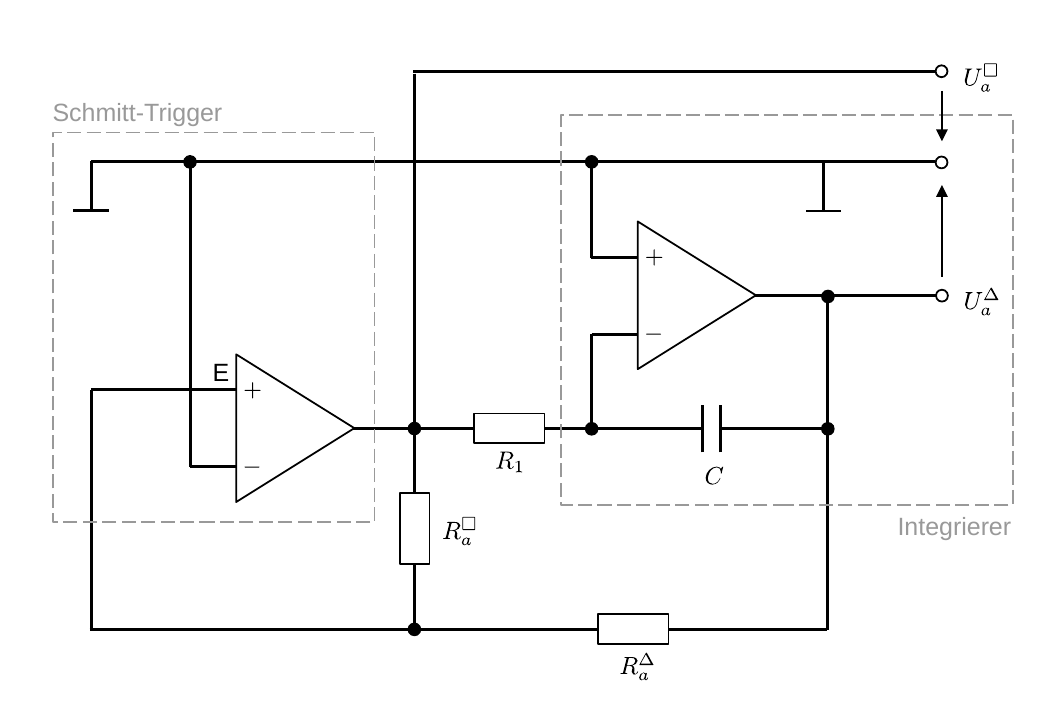
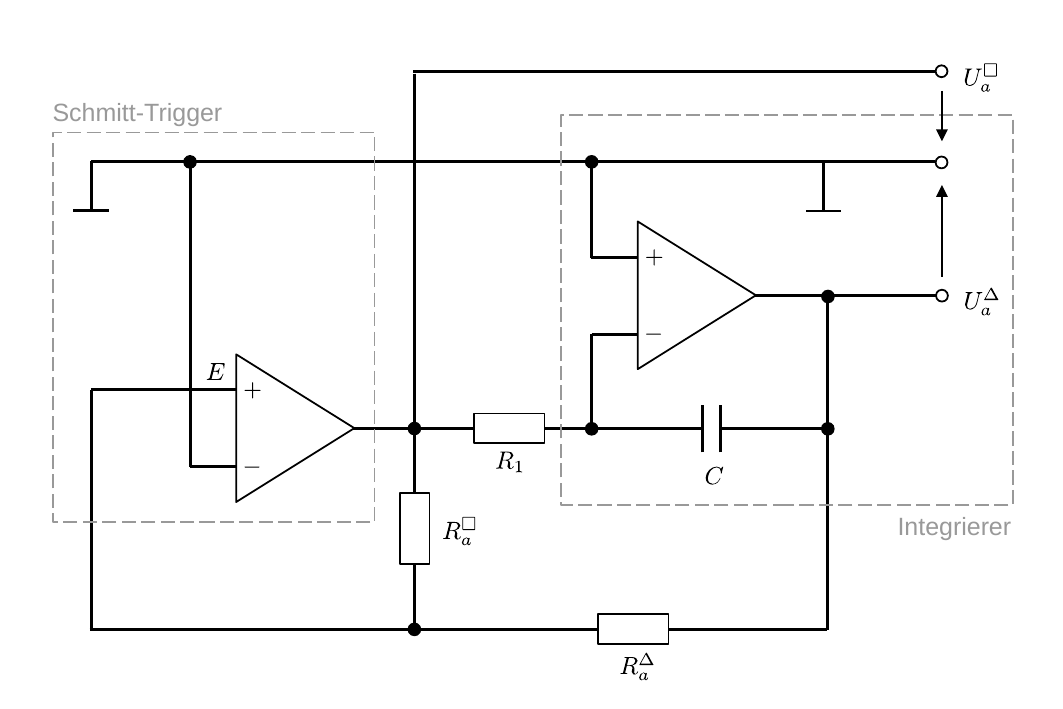
- Operationsverstaerker/figures/OPV_Generator.odg 0 additions, 0 deletionsOperationsverstaerker/figures/OPV_Generator.odg
- Operationsverstaerker/figures/OPV_Generator.png 0 additions, 0 deletionsOperationsverstaerker/figures/OPV_Generator.png
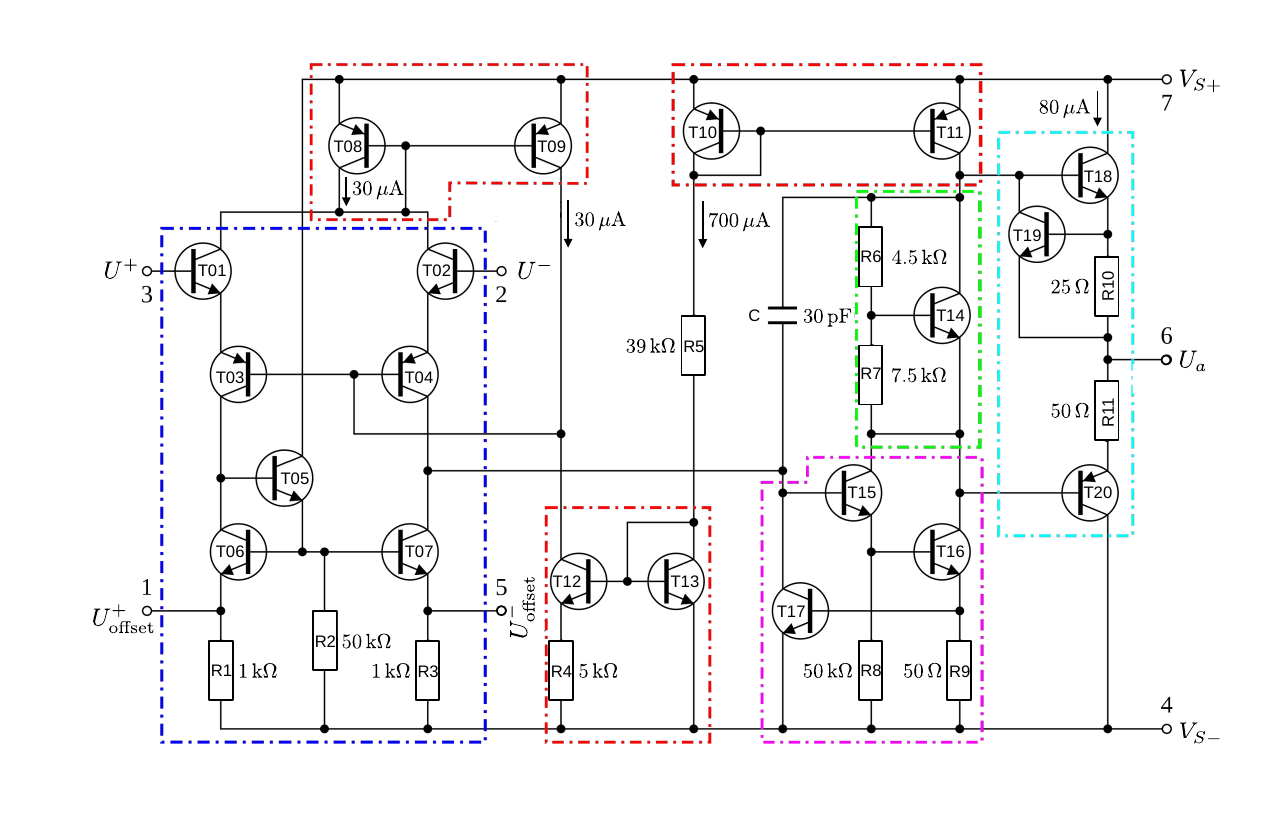
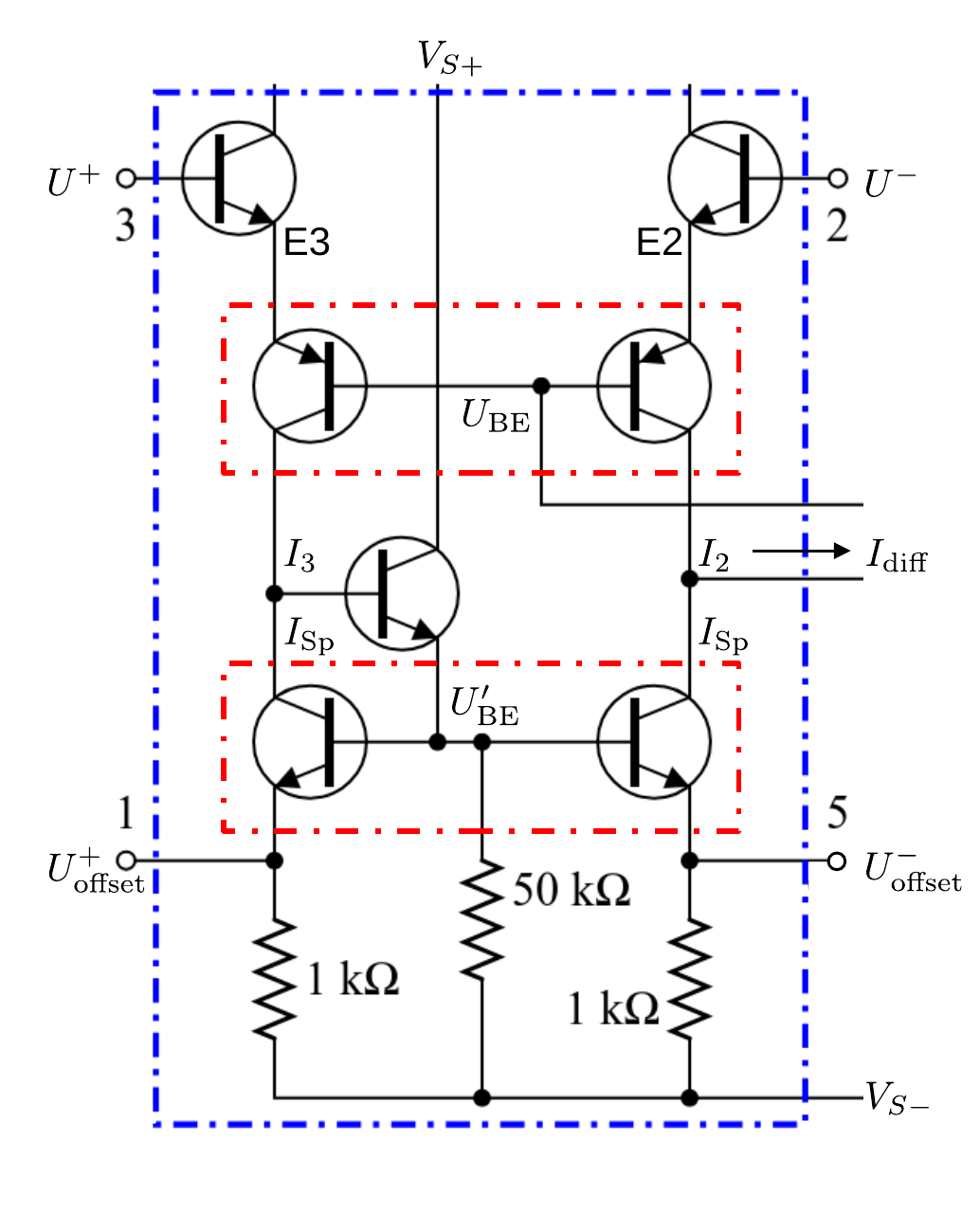
- Operationsverstaerker/figures/OPV_Innenbeschaltung.odg 0 additions, 0 deletionsOperationsverstaerker/figures/OPV_Innenbeschaltung.odg
- Operationsverstaerker/figures/OPV_Innenbeschaltung.png 0 additions, 0 deletionsOperationsverstaerker/figures/OPV_Innenbeschaltung.png
- Operationsverstaerker/figures/OPV_Verstaerkerstufe.odg 0 additions, 0 deletionsOperationsverstaerker/figures/OPV_Verstaerkerstufe.odg
- Operationsverstaerker/figures/OPV_Verstaerkerstufe.png 0 additions, 0 deletionsOperationsverstaerker/figures/OPV_Verstaerkerstufe.png
No preview for this file type
| W: | H:
| W: | H:


No preview for this file type
| W: | H:
| W: | H:


No preview for this file type
| W: | H:
| W: | H:


No preview for this file type
| W: | H:
| W: | H:


No preview for this file type
| W: | H:
| W: | H:


No preview for this file type
| W: | H:
| W: | H: