Hinweise-Komplexere-Schaltungen.md



Hinweise für den Versuch Operationsverstärker (OPV)


Komplexere Schaltungen mit Operationsverstärkern
In Aufgabe 4 werden Sie drei komplexere Schaltungen mit OPVs realisieren und studieren. Dabei handelt es sich um:

Einen idealen Einweggleichrichter;
einen Generator für Drei- und Rechtecksignale;
ein Beispiel für die analoge Lösung einer Differenzialgleichung 2. Ordnung.

Alle drei Schaltungen werden wir im folgenden kurz erklären.

Idealer Einweggleichrichter
Ein Einweggleichrichter lässt aus einem bipolaren Signal immer nur einen unipolaren Anteil durch. Die einfachste Realisation mit Hilfe einer Diode mit Durchlass für die positive Halbwelle eines sinusförmigen Eingangssignals ist in Abbildung 1 gezeigt:


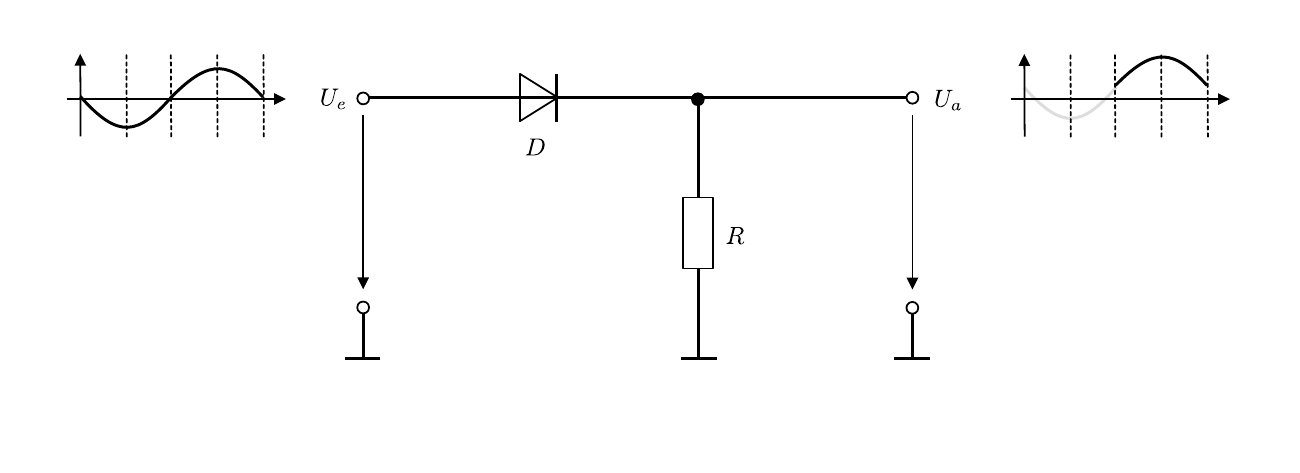
Abbildung 1: (Schaltbild eines einfachen Einweggleichrichters mit Hilfe einer Diode mit Durchlass für ein positives Signal)

Die Eingangsspannung U_{e} fällt über die Diode D und den Widerstand R ab. Das gleichgerichtete Signal kann als über R abfallende Spannung U_{a} abgegriffen werden. Ein Nachteil dieser Schaltung besteht darin, dass nicht die komplette Halbwelle des Signals wiedergegeben wird, da an der Diode immer zusätzlich die Diffusionsspannung (U_{D}\approx -0.7\ \mathrm{V} im Fall von Silizium) abfällt.
Die Schaltung eines idealen Einweggleichrichters die sich mit Hilfe eines OPV realisieren lässt und die gesamte Halbwelle wiedergibt ist in Abbildung 2 gezeigt:


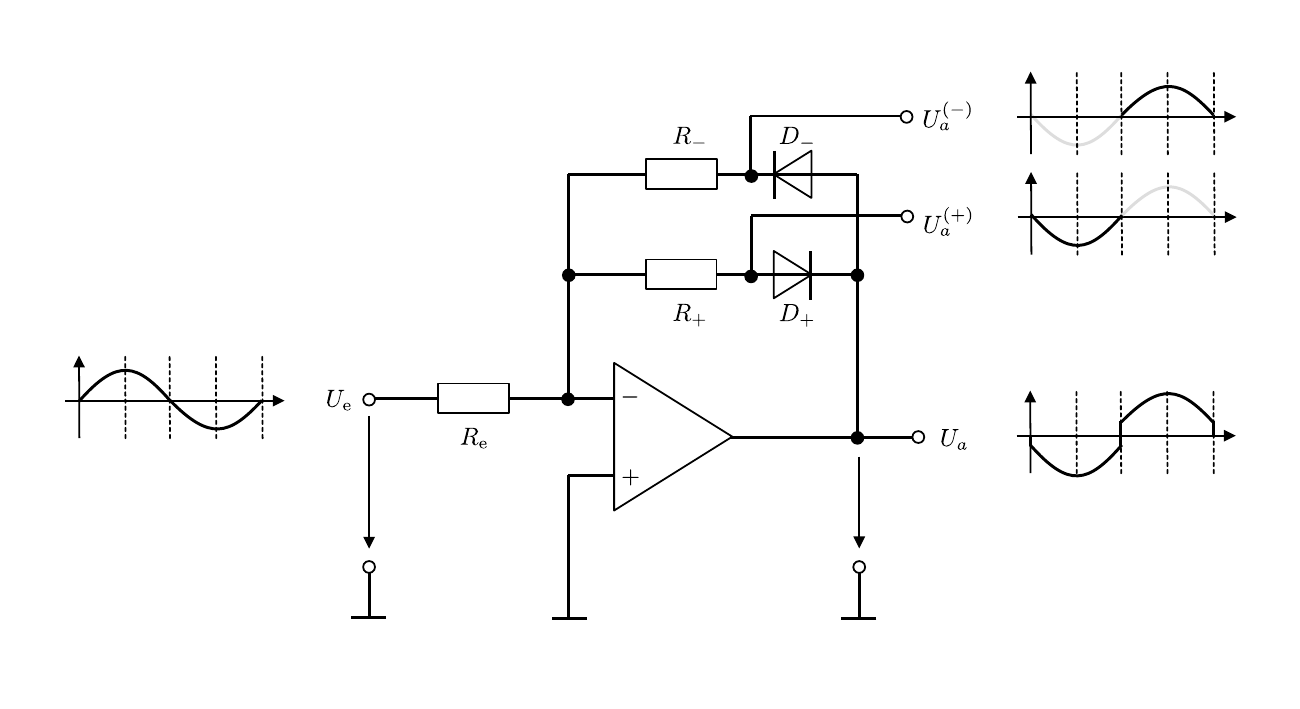
Abbildung 2: (Schaltbild eines idealen Gleichwegrichters mit Hilfe eines OPV)

Die Schaltung enthält zwei Gegenkopplungszweige, von denen je nach Vorzeichen von U_{e} immer nur einer stromführend aktiv ist.

Für U_{e}<0 sind D_{-} und R_{-} stromführend;
für U_{e}>0 sind es 𝑅_{+} und 𝐷_{+}.

Für U_{e},\ U_{a} gilt:

\begin{equation*}
\begin{split}
U_{e} = I\,R_{e};\qquad U_{a}&=I\,R_{+} - U_{D} \\
&=I\,R_{-}+U_{D}.\\
\end{split}
\end{equation*}

D_{-},\ D_{+} bewirken also einen Sprung von U_{a} um 2\ U_{D}, wenn U_{e} das Vorzeichen wechselt. Greift man U_{a}^{(+)},\ U_{a}^{(-)} jeweils vor der entsprechenden Diode ab erhält man die negative oder positive Halbwelle ohne offset.

Generator für Drei- und Rechtecksignale
Das Schaltbild eines Drei- und Rechteckgenerators ist in Abbildung 3 gezeigt:


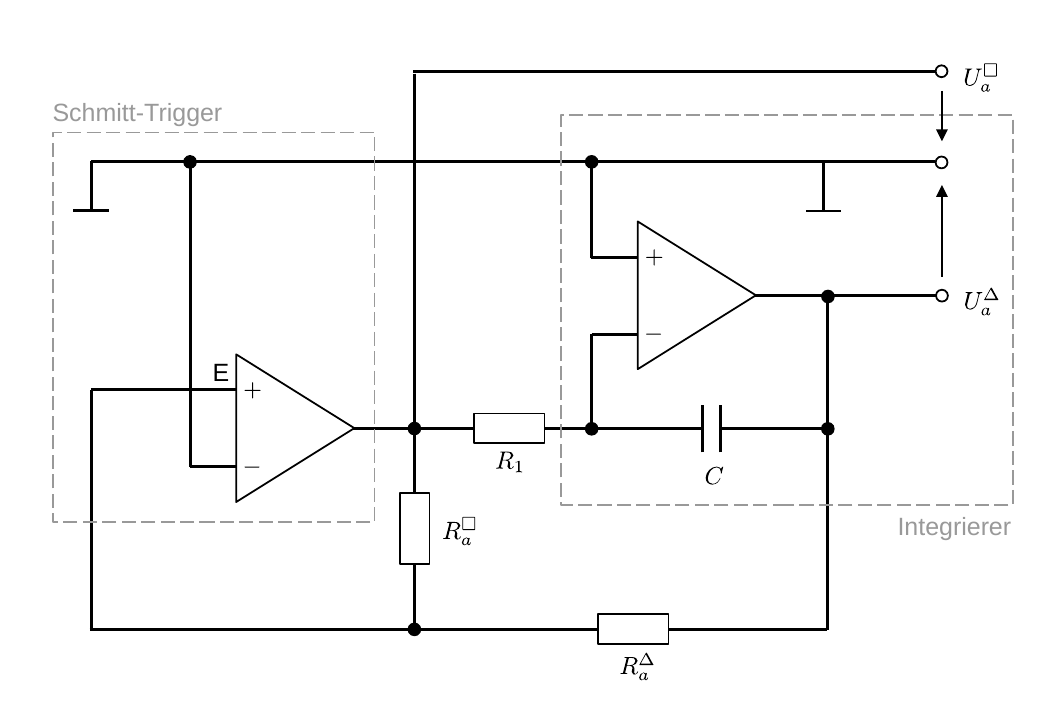
Abbildung 3: (Schaltbild eines Drei- und Rechteckgenerators mit Hilfe von zwei OPVs)

Es handelt sich dabei um eine selbsterregende Schaltung, an der kein explizites Eingangssignal anliegt; das Ausgangssignal wird allein aus den anliegenden äußeren Betriebsspannungen der OPVs abgeleitet. Dabei entstehen periodische
Ausgangssignale obwohl an den OPVs nur Gleichspannungen anliegen.
In der Schaltung fungiert der linke OPV als Schwellenwertschalter (Schmitt-Trigger) mit der Referenzspannung 0, bei dem das Ausgangssignal U_{a}^{\Box} über R_{a}^{\Box} teilweise signalverstärkend auf den P-Eingang E zurückgeführt wird. Der OPV wird ohne weitere äußere Beschaltung in Sättigung betrieben, d.h. wenn an E ein positives (negatives) Signal anliegt gibt er die vollständige positive (negative) Betriebsspannung aus.
Der OPV rechts im Bild fungiert als Integrierer (vergleiche mit Abbildung 7 hier).
Zur weiteren Klärung der Vorgänge gehen wir zunächst von einer positiven Betriebsspannung am Ausgang des Schmitt-Triggers (U_{a}^{\Box}>0) aus, die über R_{1} auf den N-Eingang des Integrierers geführt wird. Das Ausgangssignal des Integrierers ist negativ (U_{a}^{\Delta}<0) und wird über R_{a}^{\Delta} ebenfalls auf E zurückgeführt.
Zunächst wirkt auf E vor allem der (positive) Signalanteil aus U_{a}^{\Box}. Dieser Zustand besteht solange, bis C hinreichend aufgeladen ist, sodass das negative Signal aus U_{a}^{\Delta} überwiegt. Von diesem Zeitpunkt an wird U_{a}^{\Box} negativ, am Integrierer liegt ein negatives Eingangssignal an, U_{a}^{\Delta} wird positiv. Der Kondensator C wird positiv geladen und sobald der nun positive Signalanteil aus U_{a}^{\Delta} den negativen Signalanteil aus U_{a}^{\Box} an E erneut überwiegt kehrt die Schaltung in ihren ursprünglichen Zustand zurück.
An den eingezeichneten Klemmen lassen sich U_{a}^{\Delta} als periodisches Drei- und U_{a}^{\Box} periodisches Rechtecksignal abgreifen. Für den Versuch gehen wir von der folgenden Belegung der Widerstände und des Kondensators aus:

\begin{equation*}
R_{a}^{\Box}=10\ \mathrm{k\Omega}; \quad
R_{a}^{\Delta}=5.6\ \mathrm{k\Omega}; \quad
R_{1} =100\ \mathrm{k\Omega}; \quad
C  =1\ \mathrm{nF}.
\end{equation*}


Analoge Lösung einer Differentialgleichung 2. Ordnung
Eine homogene Differentialgleichung 2. Ordnung hat die Form:

\begin{equation}
\ddot{U}(t) + 2\gamma\, \dot{U}(t) + \omega_{0}^{2}U(t) = 0.
\end{equation}

Die Lösung U(t) einer solchen Differentialgleichung lässt sich mit Hilfe von zwei Integrierern und einem weiteren invertierenden Verstärker, wie in Abbildung 4 gezeigt, auf analoge Weise ermitteln:


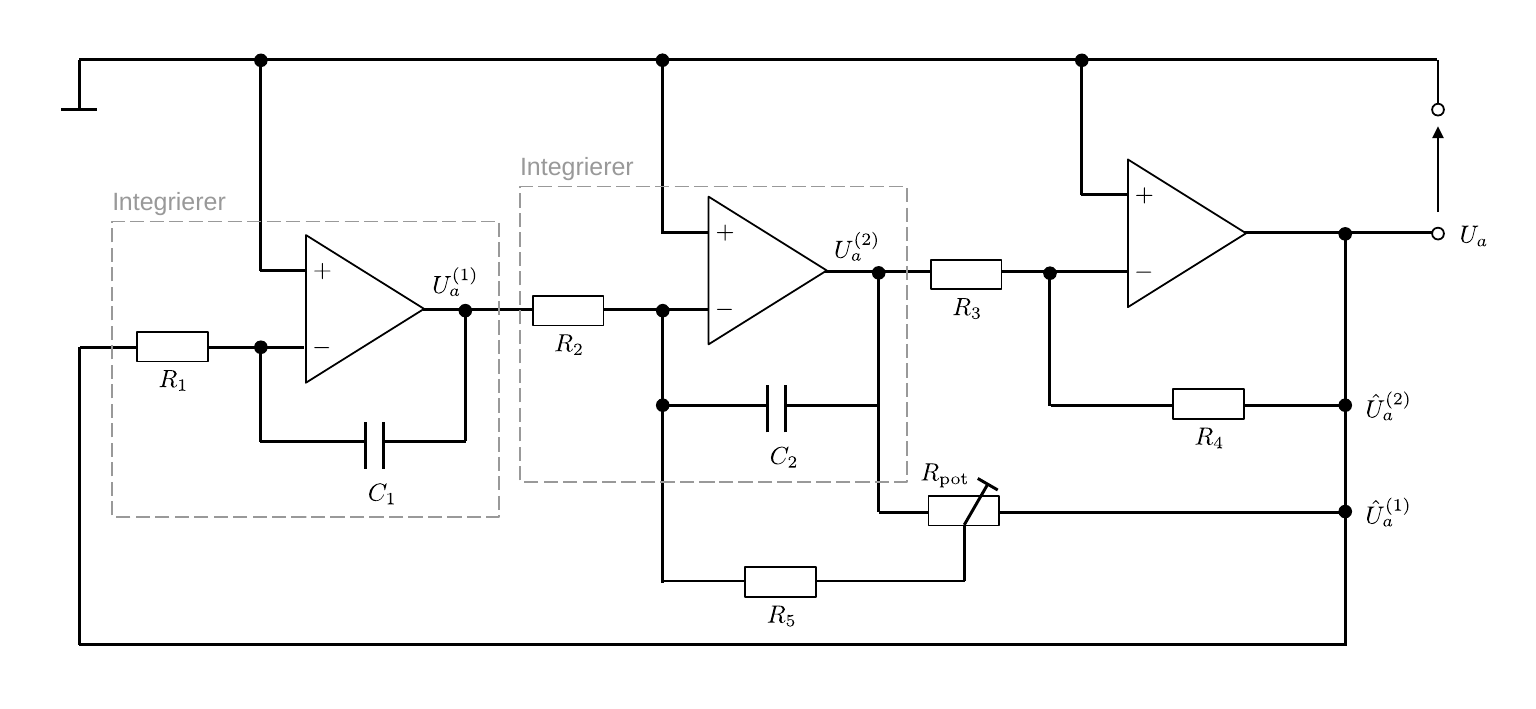
Abbildung 4: (Schaltbild zur Darstellung der Lösung einer homogenen Differenzialgleichung 2. Ordnung mit Hilfe von drei OPVs)

In der Schaltung wird U_{a} auf den N-Eingang des ersten Integrierers zurück gekoppelt. Nach Gleichung (4) hier ist das Ergebnis

\begin{equation*}
\begin{split}
& U_{a}^{(1)} = -\frac{1}{C_{1}\,R_{1}}\int U_{a}\,\mathrm{d}t.
\end{split}
\end{equation*}

Der Ausgang des ersten liegt auf dem N-Eingang des zweiten Integrierers

\begin{equation*}
\begin{split}
U_{a}^{(2)} &= -\frac{1}{C_{2}\,R_{2}}\int U_{a}^{(1)}\,\mathrm{d}t = \frac{1}{C_{2}\,R_{2}}\frac{1}{C_{1}\,R_{1}}\iint U_{a}\,\mathrm{d}t. \\
\end{split}
\end{equation*}

Auf der rechten Seite des Netzwerks addieren sich die Spannungen U_{a}, \hat{U}_{a}^{(1)} und \hat{U}_{a}^{(2)}, wobei der Symbolzusatz \hat{\cdot} kennzeichnet, dass es sich um die Anteile der Spannung nach Abzug der über die Widerstände R_{2,5,\mathrm{pot}}, bzw. R_{3,4} abgefallenen Spannungen U_{a}^{(1)} und U_{a}^{(2)} handelt. Das Symbol R_{\mathrm{pot}} steht für ein regelbares Potentiometer. Für den Versuch gehen wir von der folgenden Belegung der Widerstände und Kondensatoren aus:

\begin{equation*}
R_{1}=R_{2}=10\ \mathrm{k\Omega}; \quad
R_{3}=R_{4}=5.6\ \mathrm{k\Omega}; \quad
R_{5} =1\ \mathrm{M\Omega}; \quad
R_{\mathrm{pot}} =10\ \mathrm{k\Omega,\ (regelbar)}; \quad
C_{1}=C_{2}=470\ \mathrm{nF}.
\end{equation*}

Aus der Belegung des Netzwerks lässt sich mit Hilfe der Kirchhoffschen Regeln die Beziehung zwischen den Widerständen, Kapazitäten und Vorfaktoren \gamma und \omega_{0} aus Gleichung (1) bestimmen. Für die Durchführung des Versuchs ist dies jedoch nicht notwendig.
Dadurch, dass R_{\mathrm{pot}} regelbar ist können Sie \gamma für den Versuch variieren und den Schwing-, Kriech- und aperiodischen Grenzfall der gedämpften Schwingung experimentell einstellen.

Navigation
Main