-
- Downloads
adding new files
Showing
- Operationsverstaerker/doc/Hinweise-Innenbeschaltung.md 105 additions, 0 deletionsOperationsverstaerker/doc/Hinweise-Innenbeschaltung.md
- Operationsverstaerker/doc/Hinweise-OPV-Grundschaltungen.md 232 additions, 0 deletionsOperationsverstaerker/doc/Hinweise-OPV-Grundschaltungen.md
- Operationsverstaerker/doc/Hinweise-OPV-Komplexer-Schaltungen.md 137 additions, 0 deletions...ionsverstaerker/doc/Hinweise-OPV-Komplexer-Schaltungen.md
- Operationsverstaerker/figures/A200_DIP-8.png 0 additions, 0 deletionsOperationsverstaerker/figures/A200_DIP-8.png
- Operationsverstaerker/figures/OPVSymbolik.odg 0 additions, 0 deletionsOperationsverstaerker/figures/OPVSymbolik.odg
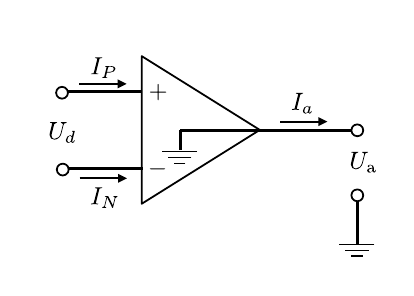
- Operationsverstaerker/figures/OPVSymbolik.png 0 additions, 0 deletionsOperationsverstaerker/figures/OPVSymbolik.png
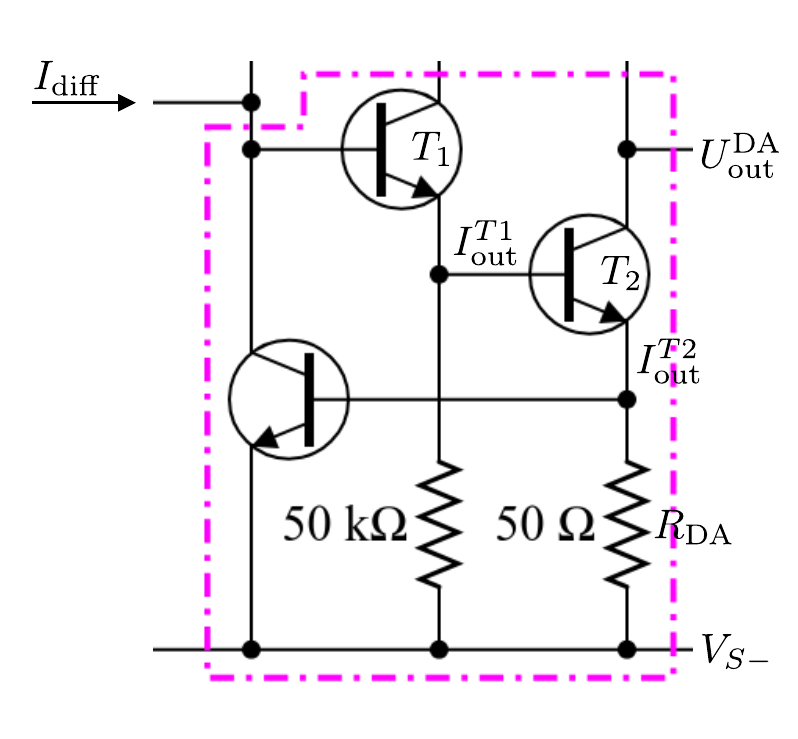
- Operationsverstaerker/figures/OPV_Ausgangsstufe.odg 0 additions, 0 deletionsOperationsverstaerker/figures/OPV_Ausgangsstufe.odg
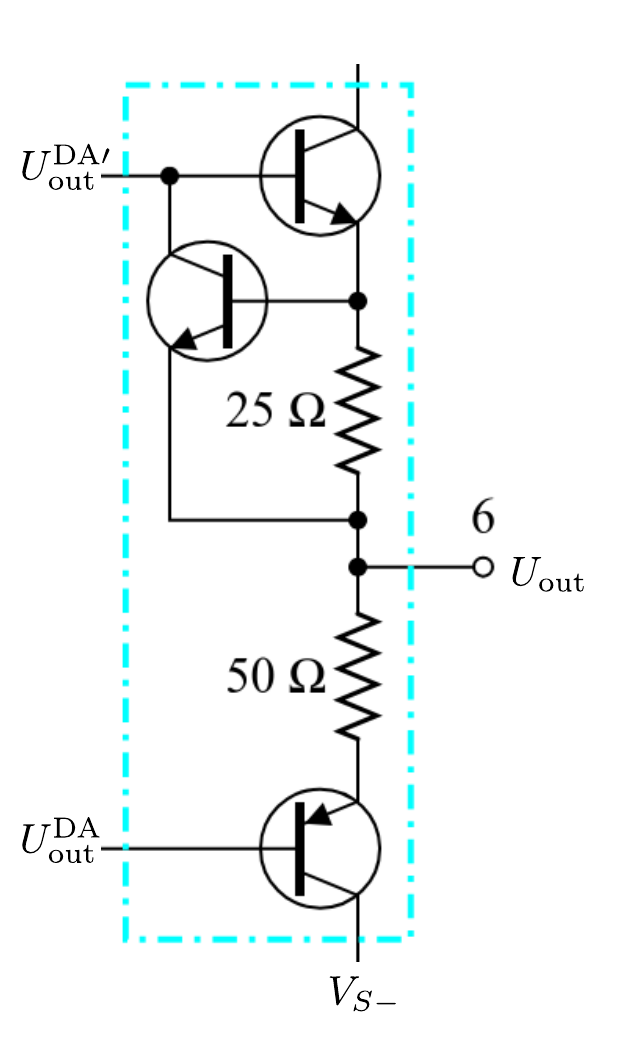
- Operationsverstaerker/figures/OPV_Ausgangsstufe.png 0 additions, 0 deletionsOperationsverstaerker/figures/OPV_Ausgangsstufe.png
- Operationsverstaerker/figures/OPV_Eingangsstufe.odg 0 additions, 0 deletionsOperationsverstaerker/figures/OPV_Eingangsstufe.odg
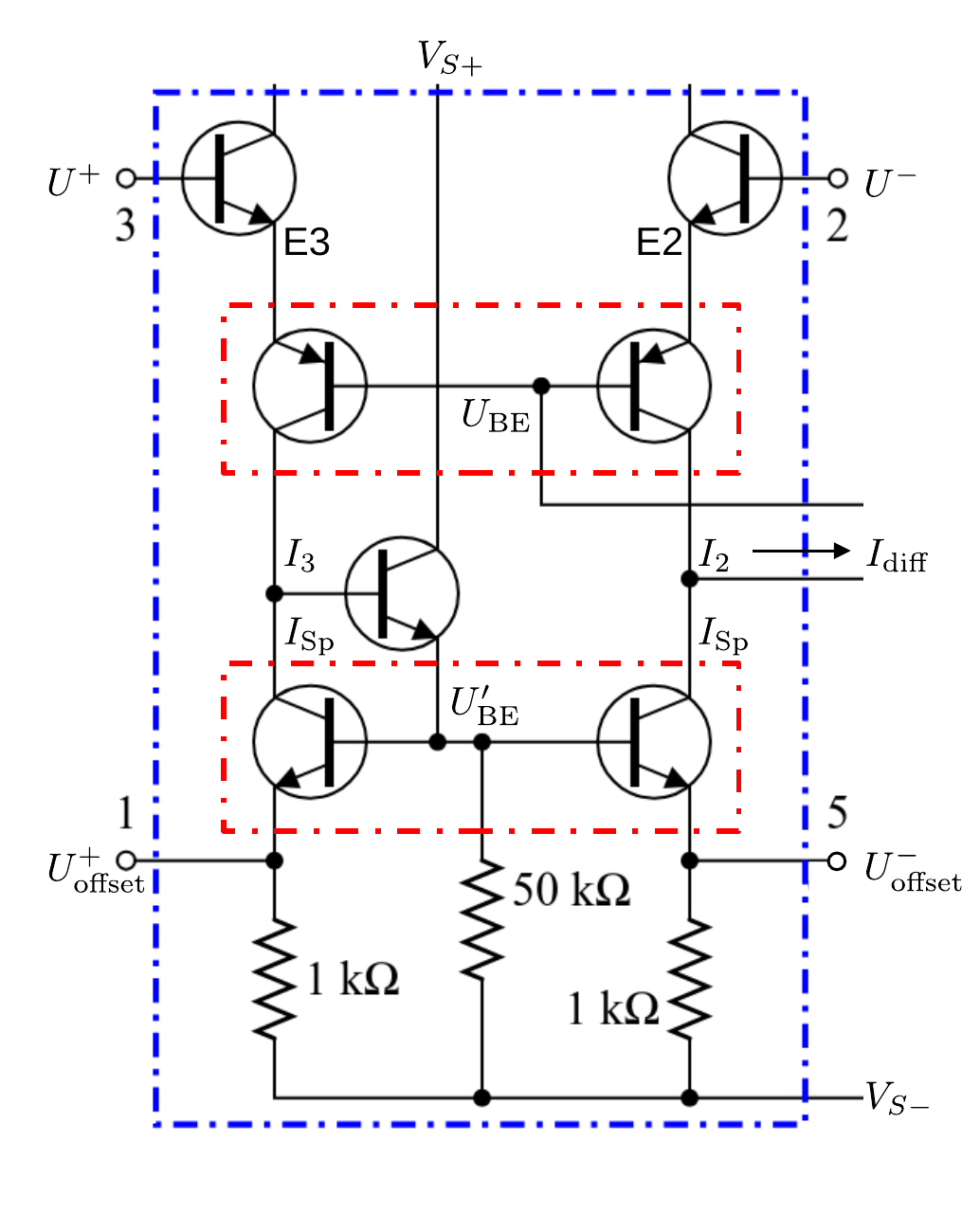
- Operationsverstaerker/figures/OPV_Eingangsstufe.png 0 additions, 0 deletionsOperationsverstaerker/figures/OPV_Eingangsstufe.png
- Operationsverstaerker/figures/OPV_Grundschaltung_inv.odg 0 additions, 0 deletionsOperationsverstaerker/figures/OPV_Grundschaltung_inv.odg
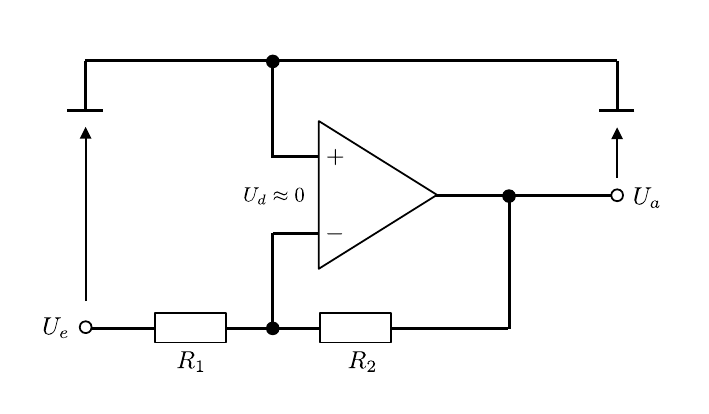
- Operationsverstaerker/figures/OPV_Grundschaltung_inv.png 0 additions, 0 deletionsOperationsverstaerker/figures/OPV_Grundschaltung_inv.png
- Operationsverstaerker/figures/OPV_Grundschaltung_ninv.odg 0 additions, 0 deletionsOperationsverstaerker/figures/OPV_Grundschaltung_ninv.odg
- Operationsverstaerker/figures/OPV_Grundschaltung_ninv.png 0 additions, 0 deletionsOperationsverstaerker/figures/OPV_Grundschaltung_ninv.png
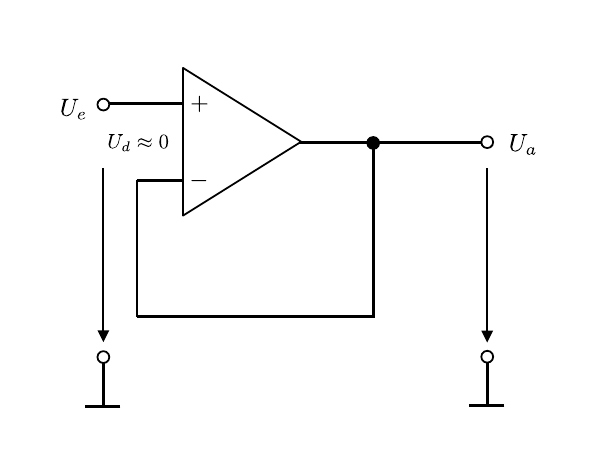
- Operationsverstaerker/figures/OPV_Impedanzwandler.odg 0 additions, 0 deletionsOperationsverstaerker/figures/OPV_Impedanzwandler.odg
- Operationsverstaerker/figures/OPV_Impedanzwandler.png 0 additions, 0 deletionsOperationsverstaerker/figures/OPV_Impedanzwandler.png
- Operationsverstaerker/figures/OPV_Verstaerkerstufe.odg 0 additions, 0 deletionsOperationsverstaerker/figures/OPV_Verstaerkerstufe.odg
- Operationsverstaerker/figures/OPV_Verstaerkerstufe.png 0 additions, 0 deletionsOperationsverstaerker/figures/OPV_Verstaerkerstufe.png
Operationsverstaerker/figures/A200_DIP-8.png
0 → 100644
655 KiB
File deleted
6.11 KiB
File added
79.5 KiB
File added
155 KiB
File added
7.88 KiB
File added
8.63 KiB
File added
6.68 KiB
File added
82.5 KiB