Hinweise-OPV-Grundschaltungen.md



Hinweise für den Versuch Operationsverstärker


Nicht-invertierender Verstärker
Beim nicht-invertierenden Verstärker (Elektrometerverstärker) handelt es sich um eine Verstärkerschaltung, bei der das Ausgangssignal die gleiche Polarität aufweist, wie das Eingangssignal. Das Eingangssignal liegt also auf dem Plus-Eingang des OPV, während der Minus-Eingang mit Masse verbunden ist. Ein Teil des Ausgangssignals wird zur Rückkopplung auf den Minus-Eingang zurückgeführt. Die Grundschaltung ist in Abbildung 1 gezeigt:


Abbildung 1: (Grundschaltung des nicht-invertierenden Verstärkers)


Verstärkung
Die Verstärkung ergibt sich aus der ersten goldenen Regel (U_{d}=0), wonach am Minus-Eingang des OPV ebenfalls U^{+} anliegt. Nach den Kirchhoffschen Regeln ergibt sich für die Spannungsverstärkung:

\begin{equation}
\begin{split}
&U_{e} = I\, R_{1};\qquad U_{a} = I\, (R_{1} + R_{2})\\
&\\
&v_{U} = \frac{U_{a}}{U_{e}} = \frac{R_{1}+R_{2}}{R_{1}} = 1+\frac{R_{2}}{R_{1}}
\end{split}
\end{equation}


Impedanzwandler
Für R_{1}\to\infty,\ R_{2}=0 wird aus der Schaltung aus Abbildung 1 eine Schaltung, wie in Abbildung 2 gezeigt:


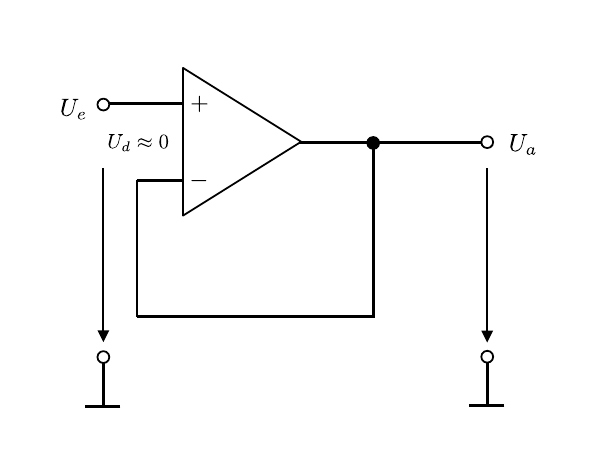
Abbildung 2: (Schaltung des Impedanzwandlers)

Nach Gleichung (1) gilt

\begin{equation*}
v_{U}=1.
\end{equation*}

Dies folgt auch wieder aus aus der ersten Goldenen Regel (U_{d}=0), wonach auf dem Minus-Eingang des OPV die gleiche Spannung U_{e}, wie am Plus-Eingang anliegt. Durch den Kurzschluss mit dem Ausgang des OPV ergibt sich U_{a}=U_{e}. Aus diesem Grund bezeichnet man die Schaltung auch als Spannungsfolger. Der Nutzen dieser Schaltung besteht darin, dass man am Ausgang des OPV die Spannung


\begin{equation*}
U_{a}=U_{e}
\end{equation*}

abgreifen kann, ohne dass es am Eingang des OPV zu einem Spannungsabfall kommt.

Eingangsimpedanz
Die Eingangsimpedanz X_{e} des OPV Schaltung lässt sich mit einer Erweiterung der Schaltung, wie in Abbildung 3 gezeigt bestimmen:


Abbildung 3: (Abbildung (b) zeigt die Schaltung zur Bestimmung von X_{e} des OPV. In Abbildung (a) ist das entsprechende Ersatzschaltbild gezeigt. Die Beschaltung innerhalb des blau gestrichelten Kastens wird im Ersatzschaltbild durch X_{e} ersetzt)

Vor den Plus-Eingang des OPV wird ein bekannter Messwiderstand R_{M} geschaltet, über den die abfallende Spannung U_{M} gemessen wird. Aus der Messung von U_{e} und U_{M}, sowie aus der Kenntnis von R_{M} lässt sich X_{e} wie folgt bestimmen:

\begin{equation}
\begin{split}
&U_{e} = I\, (R_{M}+X_{e});\qquad U_{M}=I\, R_{M}\\
&\\
&U_{e} = U_{M}\left(1+\frac{X_{e}}{R_{M}}\right);\\
&\\
&X_{e} = R_{M}\left(\frac{U_{e}}{U_{M}}-1\right).
\end{split}
\end{equation}


Ausgangsimpedanz
Die Bestimmung der Ausgangsimpedanz X_{a} des OPV ist weniger offensichtlich, da der OPV, als ein aktives Bauelement und quasi ideale Spannungsquelle, I_{a} so regelt, dass U_{a}=const. erfüllt ist. Eine statische Messung von x_{a} ist daher nicht möglich. Eine immer noch relativ einfache Methode, um X_{a} zu bestimmen ist in Abbildung 4 gezeigt:


Abbildung 4: (Abbildung (a) zeigt die Schaltung zur Bestimmung von X_{a} des OPV. In Abbildung (b) ist das entsprechende Ersatzschaltbild gezeigt. Die Beschaltung innerhalb des blau gestrichelten Kastens wird im Ersatzschaltbild durch X_{a} ersetzt)

Es ist davon auszugehen, dass X_{a} klein ist. Verbindet man den Ausgang des OPV mit einem Potentiometer mit möglichst großem, regelbarem Widerstand R_{M} mit Masse, ist davon auszugehen, dass U_{a} (bei minimaler Belastung der OPV-Ausgangs) zunächst vollständig über R_{M} abfällt. Regelt man R_{M} nun kontinuierlich nach unten, bis

\begin{equation*}
R_{M}\approx X_{a}
\end{equation*}

fällt U_{a} ab. Für den Fall R_{M}=X_{a} gilt

\begin{equation*}
\left. U_{a}\vphantom{\frac{U_{a}}{2}}\right|_{R_{M}=X_{a}} = \frac{U_{e}}{2} = \left.\frac{U_{a}}{2}\right|_{R_{M}\to\infty}.
\end{equation*}

Die entsprechende Diskussion hierzu finden Sie hier.

Invertierender Verstärker
Die Grundschaltung des invertierenden Verstärkers ist in Abbildung 5 gezeigt:


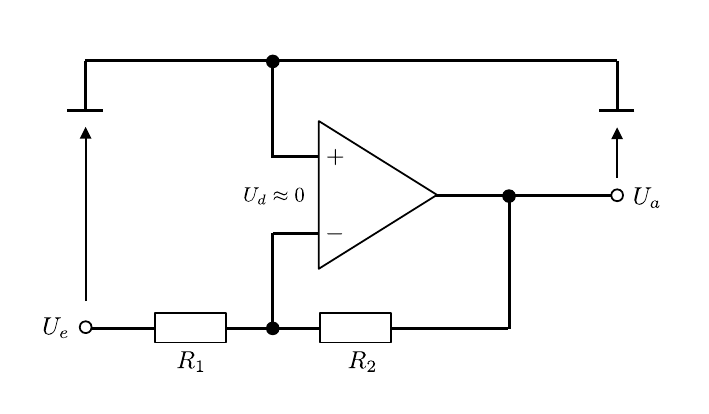
Abbildung 5: (Grundschaltung des invertierenden Verstärkers)

Das Eingangssignal liegt in diesem Fall auf dem Minus-Eingang des OPV, während der Plus-Eingang auf Masse liegt. Das Ausgangssignal U_{a} wird zur Rückkopplung teilweise auf den invertierenden Eingang zurückgeführt.
Zur Berechnung der Verstärkung verwenden wir wieder die erste goldene Regel (U_{d}=0), wonach am Minus-Eingang des OPV die gleiche Spannung anliegt, wie am Plus-Eingang. Da der Plus-Eingang jedoch auf Masse liegt muss dies auch für den Minus-Eingang gelten. Da es keine direkte Verbindung des Minus-Eingangs zur Masse gibt spricht man in diesem Fall von scheinbarer oder virtueller Masse am Minus-Eingang. Nach den Kirchhoffschen Regeln muss U_{e} vollständig über R_{1} abfallen, das gleiche gilt für U_{a} und R_{2}:

\begin{equation}
\begin{split}
&U_{e} = I\,R_{1},\qquad U_{a} = -I\,R_{2};\\
&\\
&U_{a} = -\frac{R_{2}}{R_{1}}\,U_{e}.\\
&\\
&v_{U} = \frac{U_{a}}{U_{e}} = -\frac{R_{2}}{R_{1}}
\end{split}
\end{equation}

Das Minuszeichen in Gleichung (3) folgt daraus, dass U_{a} (im Gegensatz zu U_{e}) dem Stromfluss entgegen gerichtet ist. Durch das Vorzeichen wird die Invertierung des Eingangssignals, als Phasenverschiebung um \pi (e^{i\pi}=-1) explizit sichtbar.
Im Rahmen von Aufgabe 3 werden Sie einige einfache Erweiterungen der Grundschaltung des invertierenden Verstärkers untersuchen, die wir im folgenden kurz eingeführen werden.

Addierer
Das Schaltbild des Addierers ist in Abbildung 6 gezeigt:


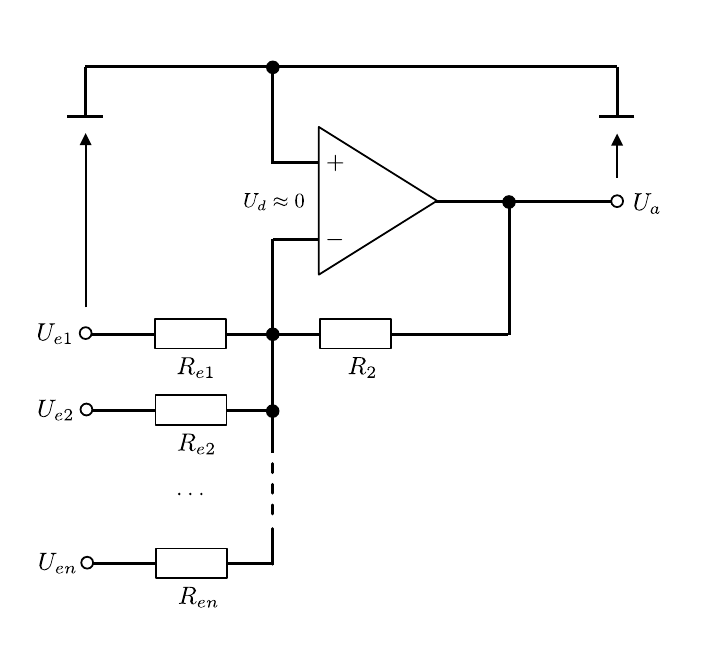
Abbildung 6: (Schaltbild des Addierers)

Die Logik folgt derjenigen zur Berechnung von v_{U} für die Grundschaltung. Im Eingangsschaltkreis addieren sich alle Teilströme zum Gesamtstrom

\begin{equation*}
I = \sum\limits_{i=1}^{n}I_{i};\qquad \text{mit}\qquad I_{i}=\frac{U_{ei}}{R_{ei}}.
\end{equation*}

Für U_{a} gilt analog zu Gleichung (3):

\begin{equation*}
\begin{split}
&U_{a} = -I\,R_{2}= -\left(\sum\limits_{i=1}^{n}{\frac{U_{ei}}{R_{ei}}}\right)\,R_{2},
\end{split}
\end{equation*}

d.h. U_{a} ist die (negative) gewichtete Summe der U_{ei}, mit den Gewichten R_{2}/R_{ei}. Belegt man alle Widerstände mit den gleichen Werten ist

\begin{equation*}
U_{\mathrm{a}}=-\sum\limits_{i=1}^{n}U_{ei}.
\end{equation*}


Integrierer
Das Schaltbild des Integrierers ist in Abbildung 7 gezeigt:


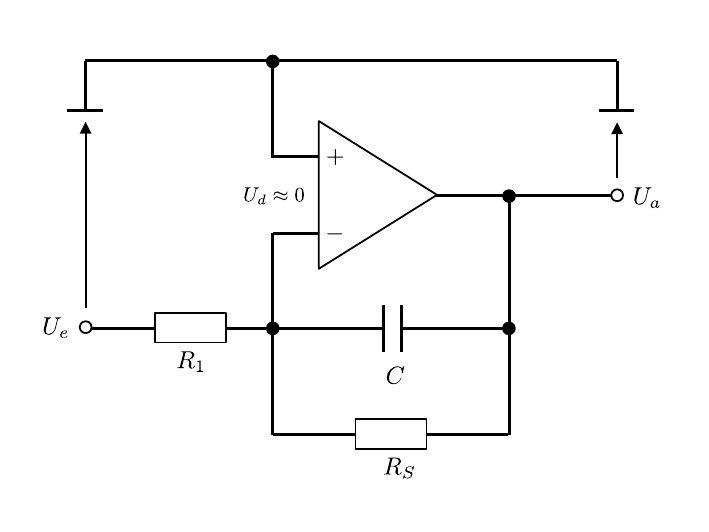
Abbildung 7: (Schaltbild des Integrierers)

Der Widerstand R_{2} aus der Grundschaltung wird in diesem Fall durch den Kondensator C ersetzt. Für U_{e},\ U_{a} gilt:

\begin{equation}
\begin{split}
& U_{e} = I\,R_{1};\qquad U_{a} = \frac{Q}{C} = -\frac{1}{C}\int I\,\mathrm{d}t = -\frac{1}{C\,R_{1}}\int U_{e}\,\mathrm{d}t,
\end{split}
\end{equation}

das Ausgangssignal entspricht also dem (negativen) Integral des Eingangssignals.
Der Widerstand R_{S} in wird in die Schaltung eingeführt, um zu verhindern, dass der Kondensator durch ein Gleichspannungssignal aufgeladen wird. Wählt man R_{S} geeignet groß, kann er (den Kirchhoffschen Regeln entsprechend) in den Betrachtungen aus Gleichung (4) vernachlässigt werden.

Differenzierer
Das Schaltbild des Differenzierers ist in Abbildung 8 gezeigt:


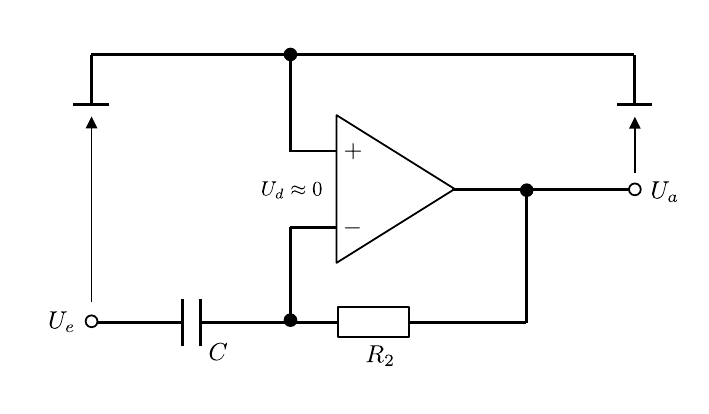
Abbildung 8: (Schaltbild des Differenzierers)

Im Vergleich zum Integrierer werden für diese Schaltung Widerstand und Kondensator vertauscht. Für das Ausgangssignal gilt:

\begin{equation*}
\begin{split}
U_{e} = \frac{Q}{C};\qquad U_{a} = -R_{2}\,I = -R_{2}\,\frac{\mathrm{d}Q}{\mathrm{d}t} = -&\underbrace{C\,R_{2}\vphantom{\frac{\mathrm{d}U_{e}}{\mathrm{d}t}}}\frac{\mathrm{d}U_{e}}{\mathrm{d}t},\\
&\equiv\tau
\end{split}
\end{equation*}

das Ausgangssignal entspricht also der (negativen) Ableitung des Eingangssignals. Das Produkt \tau=C\ R_{2} wird als Zeitkonstante bezeichnet.

Essentials
Was Sie ab jetzt wissen sollten:

Sie sollten die Grundschaltungen des invertierenden und des nicht-invertierenden Verstärkers kennen.
Sie sollten die Schaltung des OPV als Impedanzwandler kennen und mindestens ein Verfahren in Erinnerung haben, wie man X_{e} und X_{e} des OPV messen kann.
Sie sollten die Grundschaltungen des OPV mit Hilfe der Goldenen Regeln zur Dimensionierung von OPV Schaltungen erklären können.


Testfragen

Wo liegt das Problem bei dere Messung von X_{a} des OPV? Warum haben Sie dieses Problem bei der Messung von X_{e} nicht?
Ihr Signal besteht aus einer geringen Aufladung eines Kondensators. Was passiert, wenn Sie versuchen diese Aufladung als Spannungsantieg mit einem Spannungsmessgerät mit moderatem Innenwiderstand zu messen?
Wie würden Sie das Signal durch einen OPV vom Spannungsmessgerät entkoppeln?


Navigation
Main