-
Roger Wolf authoredRoger Wolf authored
Hinweise für den Versuch Polarisation und Doppelbrechung
Polarisation
Lineare, elliptische und zirkulare Polarisation
Elektromagnetsiche (em) Wellen sind transversale Wellen. Ihre Polarisation wird i.a. durch die Ausrichtung des elektrischen Feldstärkevektors \vec{E} definiert. Zur besseren Übersicht stellen wir für die weitere Diskussion o.B.d.A. die Welle durch ihre zeitliche Entwicklung in \vec{E}(t) mit der festen Kreisfrequenz \omega und der festen Wellenzahl \vec{k} dar. Wir betrachten die Welle außerdem an einem festen Ort in der Ebene senkrecht zu \vec{k}. Für linear polarisierte Wellen variiert \vec{E}(t) entlang einer Achse mit zeitlich unveränderlicher Orientierung in dieser Ebene:
\begin{equation*}
\vec{E}(t) = \vec{E}\,e^{\pm i\omega\,t}.
\end{equation*}
Jede linear polarisierte Welle mit der Amplitude \vec{E} lässt sich in zwei senkrecht zueinander stehende, linear polarisierte Teilwellen mit den Amplituden \vec{E}_{1}\perp\vec{E}_{2}, wie in Abbildung 1 dargestellt, zerlegen:
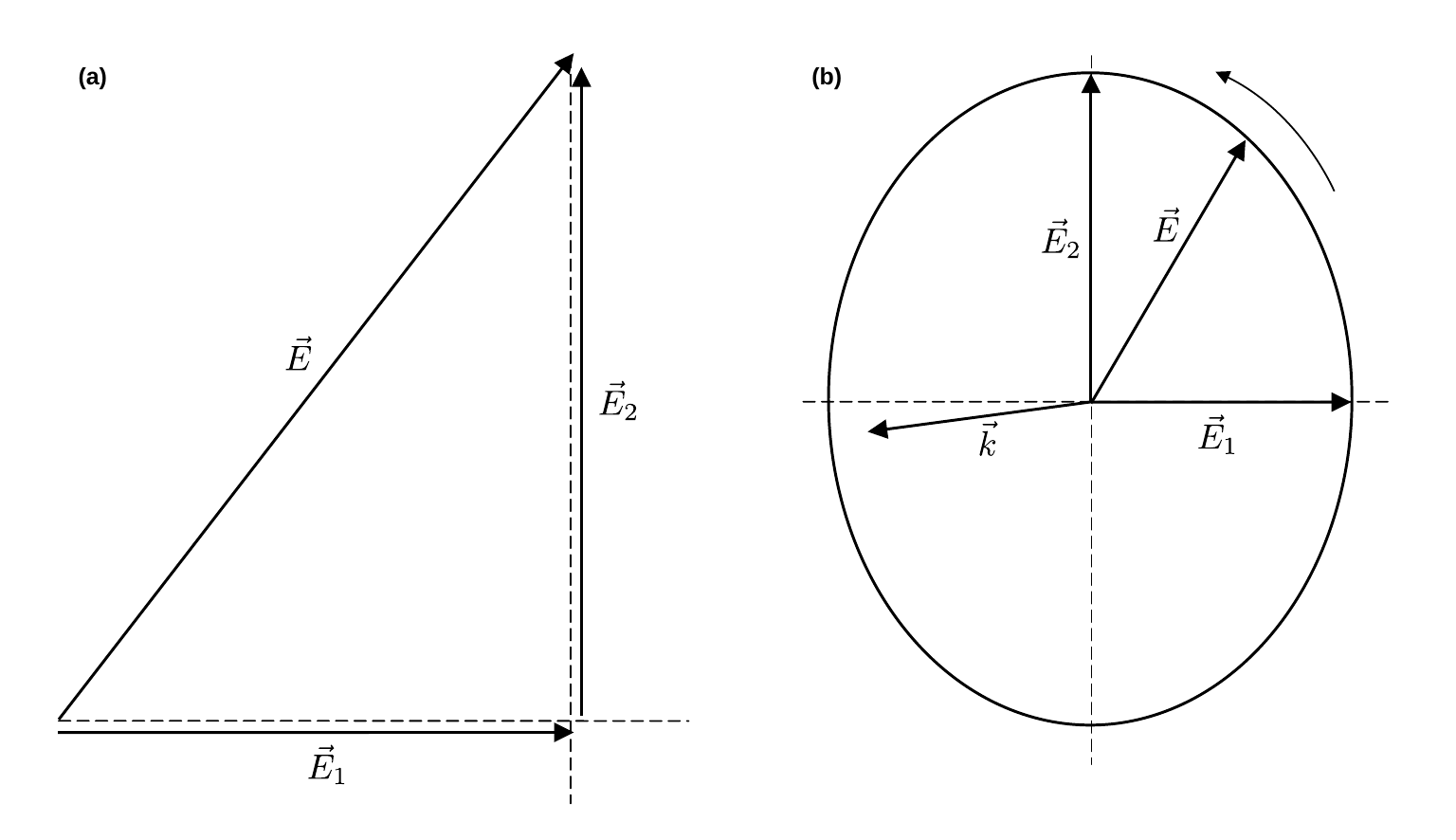
Abbildung 1: (Bild (a) zeigt die Aufspaltung des Vektors \vec{E} in zwei senkrecht zueinander stehende Komponenten \vec{E}_{1}\perp \vec{E}_{2}. Bild (b) zeigt den Fall der elliptischen Polarisation, wobei zwischen den ebenen Teilwellen zu \vec{E}_{1} und \vec{E}_{2} eine Phasendifferenz von \Delta\phi=\pi/2 besteht
Je nachdem welche weiteren Randbedingungen für die Beträge |\vec{E}_{1}| und |\vec{E}_{2}| und die Phasenbeziehung \Delta\phi\in[0,\pi) zwischen den Wellen \vec{E}_{1}(t) und \vec{E}_{2}(t) besteht weist \vec{E}(t) eine unterschiedliche Polarisation auf: