Hinweise-Piezoeffekt.md



Hinweise für den Versuch Elektrische Bauelemente


Druckabhängige Bauelemente
Stoffe bei denen es unter der Einwirkung gerichteter mechanischer Spannung zur elektrischen Polarisation kommt bezeichnet man als piezoelektrisch. Man bezeichnet diesen Effekt als den direkten piezoelektrischen Effekt oder direkten Piezoeffekt. Umgekehrt verformen sich piezoelektrische Stoffe, wenn elektrische Spannungen an ihnen anliegen. Diesen Effekt bezeichnet man als inversen Piezoeffekt.
Der Piezoeffekt tritt bei Stoffen auf, die polare Bindungen besitzen und deren Kristallstruktur Elementarzellen (EZ) ohne Punktsymmetrie am Zentrum der EZ aufweisen, wie dies z.B. bei Quarz (\mathrm{SiO_{2}}) der Fall ist. Eine vereinfachte Darstellung der Geometrie für Quarz ist in Abbildung 1 gezeigt:


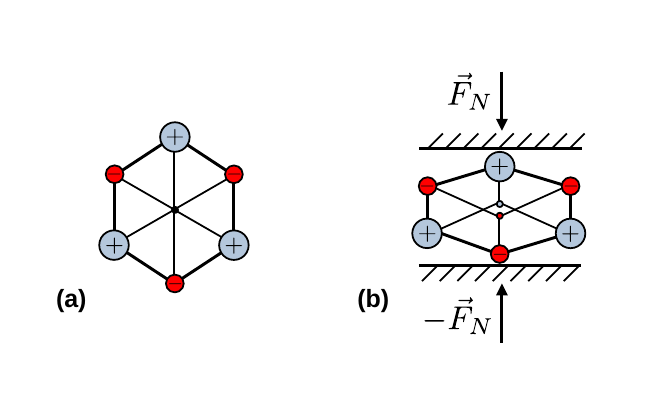
Abbildung 1: (Ein hexagonal nicht punktsymmetrsicher Schnitt durch Quarz, für den es unter mechanischer Spannung zum direkten Piezoeffekt kommt. Abbildung (a) zeigt eine EZ des Kristall ohne äußere, mechanische Spannungseinwirkung. Abbildung (b) zeigt die gleiche EZ unter einer äußeren, mechanischen Spannungseinwirkung)

Im Quarz bildet das vierwertige Si zwei polare Doppelbindungen mit zwei Sauerstoffatomen aus. Die Kristallstruktur weist einen Schnitt auf, entlang dessen sich eine hexagonale Struktur in einer Helix durch den Kristall windet, mit einer EZ, wie in Abbildung 1 (a). Diese weist keine Punktsymmetrie an ihrem Zentrum auf, ein Sauerstoffatom wird jeweils im Zentrum auf ein Si-Atom abgebildet und umgekehrt. Die Ladungsschwerpunkte der Sauerstoffatome (in rot) und der Si-Atome (in blau) fallen aufeinander, so dass der Kristall keine Nettopolarisation aufweist. Unter der Einwirkung einer gerichteten Spannung, wie in Abbildung 1 (b) gezeigt, verschieben sich die Ladungsschwerpunkte und es kommt zur Polarisation die, in diesem Fall an den Oberflächen des Kristalls, auf die die Spannung jeweils ausgeübt wird zur Ladungstrennung und damit zu einer Spannung führt.
Im Gegenzug führt das Anlegen einer elektrischen Spannung (im Bild mit positiver Polung oben und negativer Polung unten) zu einer Abflachung des Kristalls in der angegebenen Richtung. Dieser Längs-Effekt ist am einfachsten zu beschreiben. Je nach Kristallstruktur kann es aber auch zu Quer- und Scher-Effekten kommen.
Die mathematische Beschreibung erfolgt z.B. effektiv, d.h. ohne Berücksichtigung der mikroskopischen Strktur im Rahmen der Kontinuumsmechanik in erster Näherung durch die Gleichung:

\begin{equation*}
P=d\,T = e\,S,
\end{equation*}

wobei P der Polarisation des Kristalls, T der mechanischen Spannung und S der relativen Verformung entsprechen. Bei den

\begin{equation*}
d_{ijk} = \frac{\partial S_{ij}}{\partial E_{k}}
\end{equation*}

handelt es sich um die piezoelektrischen Verzerrungskoeffizienten. Bei den

\begin{equation*}
e_{ijk} = \frac{\partial T_{ij}}{\partial E_{k}}
\end{equation*}

handelt es sich um die piezoelektrischen Spannungskoeffizienten. Beide lassen sich jeweils zu einem Tensor dritter Stufe anordnen.

Funktionsweise einer Quarzuhr
Die Funktionsweise einer Quarzuhr beruht auf dem Piezoeffekt von Quarz. Im Werk wird ein Resonator, wie eine Stimmgabel, auf eine Eigenfrequenz

\begin{equation*}
\nu_{0}=32.768\,\mathrm{kHz}
\end{equation*}

kalibriert. Dies erfolgt unter Auftragung dünner Goldschichten, um die Trägheit des Resonators zu erhöhen, bis die gewünschte Eigenfrequenz erreicht ist. Bei \nu_{0} handelt es sich um die niedrigste Zweierpotenz

\begin{equation*}
2^{15}=32768
\end{equation*}

oberhalb des Frequenzbereichs von {\approx}20\ \mathrm{kHz}, ab dem das menschliche Ohr Frequenzen nicht mehr wahrnimmt. Die Uhr macht dadurch beim Betrieb keine wahrnehmbaren Geräusche. In der Uhr wird die Spannung aufgrund des piezoelektrischen Effekts abgegriffen und durch einen Operationsverstärker positiv auf den Kristall zurück gekoppelt, was den Quarz zur resonanten Schwingung anregt. Die Schwingung wird durch die Toggle-Zustände von 15 in Reihe geschaltete Jack-Kilby Flipflops (JK-FF) 15 mal halbiert, woraus sich eine Schwingung von einer Sekunde einstellt.
Sehr gute Quarzuhren verlieren auf einen Tag nicht mehr als 5 Sekunden, was einer Präzision von besser als 6\times10^{-5} entspricht.

Navigation
Main