Hinweise-Leiter-Halbleiter-Isolatoren.md



Hinweise für den Versuch Elektrische Bauelemente


Energieniveaus in Atom und Festkörper
Im Atom besetzen die Elektronen der Hülle Orbitale mit diskreten Energieniveaus. Aufgrund des Pauli-Prinzips kann jedes Energieniveau nur durch eine endliche Anzahl von Elektronen besetzt werden. In Molekülen spalten die Energieniveaus z.B. aufgrund zusätzlicher Rotations- und Vibrationsfreiheitsgrade auf. Im Übergang zum Festkörper (FK) nimmt diese Aufspaltung weiter zu, so dass sich (für eine Anzahl von Basisatomen (BA) eines FK in der Größenordnung von N_{A}) quasi-kontinuierliche Energiebänder ausbilden. Es handelt sich dabei immer noch um eine wenn auch sehr große Zahl diskreter Energieniveaus, die in bestimmten Bereichen sehr eng beieinander liegen. Dieser Übergang ist in Abbildung 1 schematisch dargestellt:


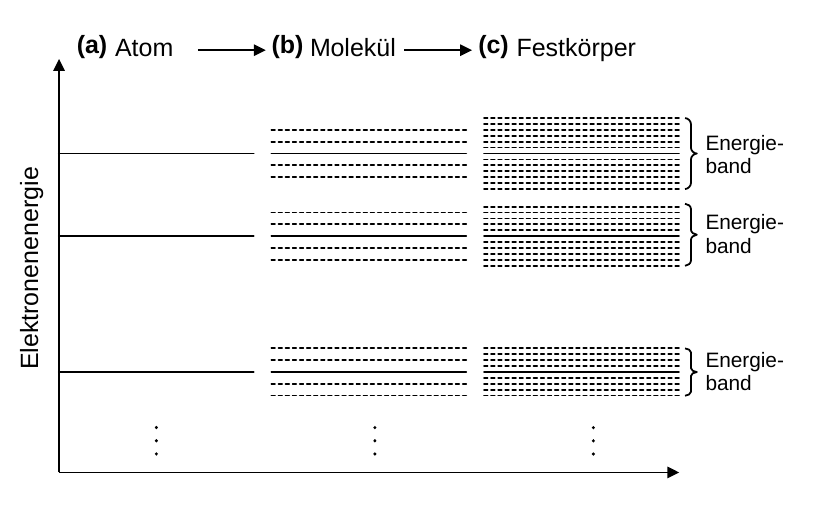
Abbildung 1: (Übergang von den Energieniveaus eines einzelnen Atoms (a) über die Energieniveaus eines Moleküls (b) bis zu den quasi-kontinuierlichen Energiebändern im FK (c))

Nach wie vor gilt für die Elektronen im FK das Pauli-Prinzip, so dass jedes einzelne Energieniveau nur durch eine endliche Anzahl von Elektronen besetzt werden kann. Zwischen den Energiebändern bilden sich verbotene Bereiche aus, deren Energieniveaus von Elektronen im FK nicht angenommen werden können.
Durch thermische Anregung nimmt der FK Energie aus seiner Umgebung auf, so dass sich Elektronen auch in höheren (jedoch erlaubten) Energieniveaus, als im Grundzustand des FK befinden können. Die Wahrscheinlichkeit dafür bei der Temperatur T des FK ein Elektron mit der Energie E anzutreffen ist durch die Boltzmann-Statistik

\begin{equation*}
p = \frac{1}{Z}e^{-E/k_{\mathrm{B}}T}
\end{equation*}

gegeben, wobei k_{\mathrm{B}} die Boltzmann-Konstante und Z eine Normierungskonstante sind. Für das Produkt k_{\mathrm{B}}T gilt

\begin{equation*}
\left.k_{\mathrm{B}}T\right|_{T=300\,\mathrm{K}} = 0.0258\,\mathrm{eV}.
\end{equation*}

Ein Elektron kann jedoch nur dann thermisch angeregt werden, wenn die Anregung den Gesetzen der Energie-Impulserhaltung folgt und der Energiezustand nach Anregung durch das Pauli-Prinzip erlaubt ist.
Für die Temperatur T_{0}=0\ \mathrm{K} sind alle Energiezustände vom niedrigsten bis zu einem maximalen Energieniveau durch die Elektronen des FK besetzt. Diese maximale Energie bezeichnet man als Fermi-Energie E_{F}. Das höchste (bei T_{0}) durch Elektronen vollständig besetzte Band bezeichnet man als Valenzband. Es ist durch die Valenzelektronen der BA besetzt. Das niedrigste nicht vollbesetzte Band bezeichnet man als Leitungsband. Das Valenz- und das Leitungsband bestimmen die elektronischen Eigenschaften des FK, die Sie in diesem Versuch an verschiedenen elektrischen Bauelementen untersuchen.

Leitfähigkeit im Festkörper
Im FK sind die BA fest in einem periodischen Gitter, dem Kristall, gebunden. Das genaue Aussehen dieses Gitters wird durch die elektronischen Eigenschaften, wie z.B. die Wertigkeit, der BA bestimmt. Bis zum Valenzband sind die Elektronen fest an die BA gebunden. Im Leitungsband besteht diese lokale Bindung nicht mehr, so dass sich die Elektronen im Leitungsband frei durch den FK bewegen können (freies Elektronengas). Wechselt ein Elektron, z.B. durch thermische Anregung vom Valenz- ins Leitungsband hinterlässt es im Gitter den ionisierten Rumpf eines BA, der in diesem Fall auch als Loch oder Defektelektron bezeichnet wird. Die Leitfähigkeit eines FK für elektrischen Strom wird durch die Anzahl der Elektronen im Leitungsband bestimmt, die im Idealfall (d.h. bei einem FK mit ungestörter Gitterstruktur) zur Anzahl der Löcher äquivalent ist.
Der Transport elektrischer Ladung findet in der Realität nur durch die Elektronen im Leitungsband statt, da die Rümpfe der BA fest in der Gitterstruktur verankert sind. Die Bewegung der Elektronen ist jedoch mit der Interpretation einer (Quasi-)Bewegung von Löchern entgegen der Elektronenbewegung im Valenzband äquivalent.
Die vereinfachte Beschreibung des FK durch Valenz- und Leitungsband erfolgt im Bändermodell. Im Rahmen dieses Modells lassen sich alle FK bezüglich ihrer Leitfähigkeit in drei Klassen einteilen:

Beim Leiter überlappen Valenz- und Leitungsband. Ein Leiter besitzt eine hohe Leitfähigkeit.
Beim Isolator ist die Lücke (engl. gap) E_{g} zwischen Valenz- und Leitungsband so groß, dass sie für ein einzelnes Elektron nicht einfach aufgebracht werden kann (E_{g}>3\ \mathrm{eV}). Ein Isolator ist i.a. nicht leitend.
Dazwischen liegt der Halbleiter, bei dem die Lücke zwischen Valenz- und Leitungsband mit 1<E_{g}<3\ \mathrm{eV} klein ist.  Ein Halbleiter besitzt eine geringe (intrinsische) Leitfähigkeit.

Diese Einordnung von FK in Leiter, Isolatoren und Halbleiter ist in Abbildung 2 schematisch dargestellt:


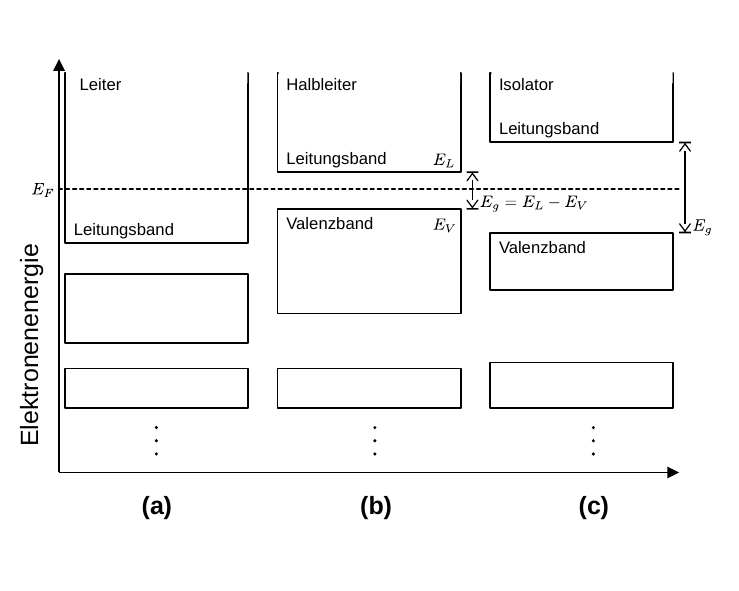
Abbildung 2: (Schematische Einteilung des FK in (a) Leiter, (b) Halbleiter und (c) Isolator im Bändermodell)