-
Roger Wolf authoredRoger Wolf authored
Hinweise für den Versuch Kreisel
Aufgabe 2: Kardanisch gelagerter Kreisel [2/4]
Die obigen Betrachtungen gelten für einen einfachen symmetrischen Kreisel. Im Fall des in (Abbildung 1 hier) gezeigten, kardanisch gelagerten Kreisels, wie er im Praktikum zum Einsatz kommt, müssen die Trägheitsmomente der massiven Kardanrahmen bei der Beschreibung der Kreiselbewegung berücksichtigt werden. Bei Drehungen um \hat{x} dreht sich der innere, bei Drehungen um \hat{y} sowohl der innere, als auch der äußere Kardanrahmen mit. Für die Trägheitsmomente gilt daher: \begin{equation*} \begin{split} &\theta_{x}^{\prime} = \theta_{x} + \theta_{x}^{(i)} + \theta_{x}^{(a)}; \\ &\theta_{y}^{\prime} = \theta_{y} + \theta_{y}^{(i)}; \\ &\theta_{z}^{\prime} = \theta_{z}, \\ \end{split} \end{equation*} wobei \theta_{x}=\theta_{y}=\theta_{\perp} die Trägheitsmomente des Rotors, \theta_{x}^{(i)} und \theta_{y}^{(i)} die Trägheitsmomente des inneren und \theta_{x}^{(a)} das Trägheitsmoment des äußeren Kardanrahmens sind. Unter diesen Voraussetzungen ergibt sich für kleine Werte von \beta \begin{equation} \omega_{N} = \omega\,\frac{\theta_{z}^{\prime}}{\sqrt{\theta_{x}^{\prime}\,\theta_{y}^{\prime}}} \end{equation}
Präzession
Zur Diskussion der Präzession betrachten wir einen symmetrischen Kreisel, der mit der Winkelgeschwindigkeit \vec{\omega} um die Figurenachse \hat{z} rotiert. Die zugehörige Geometrie zu diesen Betrachtungen ist in Skizze 6 gezeigt. Da der Kreisel um die Figurenachse rotiert gilt \vec{L}=\theta_{z}\,\vec{\omega}. Im Abstand \vec{r}=r\hat{z} soll ein zusätzliches Gewicht dazu führen, dass auf den Kreisel ein resultierendes Drehmoment \begin{equation} \vec{M} = \vec{r}\times\vec{F}_{g}; \qquad M=m\,g\,r\sin\gamma \end{equation} wirkt.
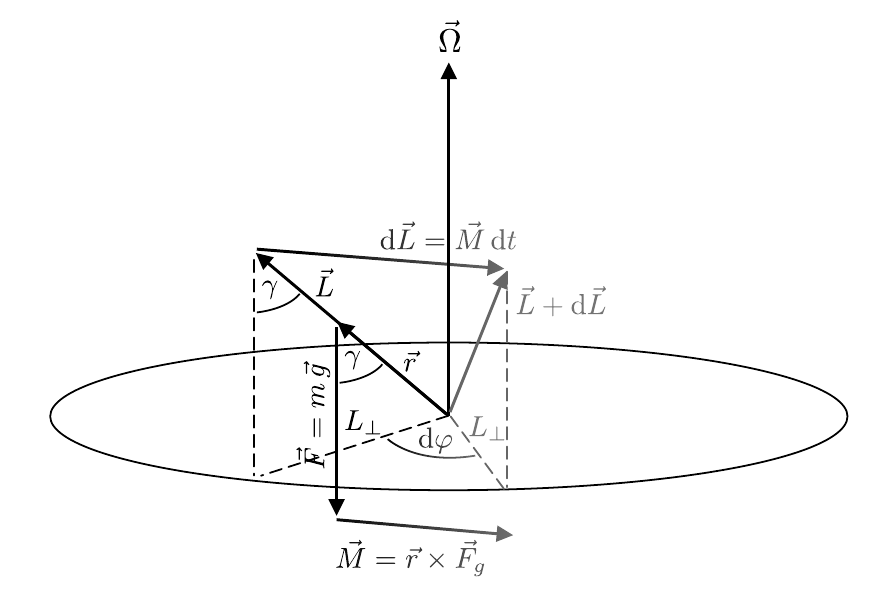
Skizze 6 (Geometrie eines präzedierenden Kreisels)
Nach einem Zeitabschnitt \mathrm{d}t führt \vec{M} zu einer Änderung \begin{equation*} \mathrm{d}\vec{L} = \vec{M}\,\mathrm{dt}. \end{equation*} Da \vec{L} per Konstruktion parallel zu \vec{r} verläuft, gilt nach Gleichung (2) \vec{M}\perp\vec{L}, d.h. \mathrm{d}\vec{L} ändert die Richtung, nicht aber den Betrag von \vec{L}. Diese Änderung führt zu einer Drehung von \vec{L} um den Winkel \begin{equation*} \mathrm{d}\varphi = \frac{\mathrm{d}L}{L_{\perp}} = \frac{M\,\mathrm{d}t}{L\sin\gamma} \end{equation*} und damit zu einer Rotation des Kreisels mit der Winkelgeschwindigkeit \begin{equation} \Omega = \frac{\mathrm{d}\varphi}{\mathrm{d}t} = \frac{M}{L\sin\gamma} = \frac{m\,g\,r\,\sin\gamma}{\theta_{z}\,\omega\,\sin\gamma} = \frac{m\,g\,r}{\theta_{z}\,\omega}. \end{equation} Unter Berücksichtigung der Vektorstruktur ergibt sich \begin{equation} \vec{M}=\vec{\Omega}\times\vec{L}. \end{equation}
Kreiselkompass
Der Kreiselkompass, wie er im P1 zu Demonstrationszwecken verwendet wird, ist ebenfalls kardanisch gelagert, jedoch ist der innere Kardanrahmen durch Schraubenfedern an den äußeren Kardanrahmen gebunden. Die Funktionsweise eines Kreiselkompasses ist in Skizze 7 gezeigt, in der die Nordhalbkugel der Erde schematisch dargestellt ist:
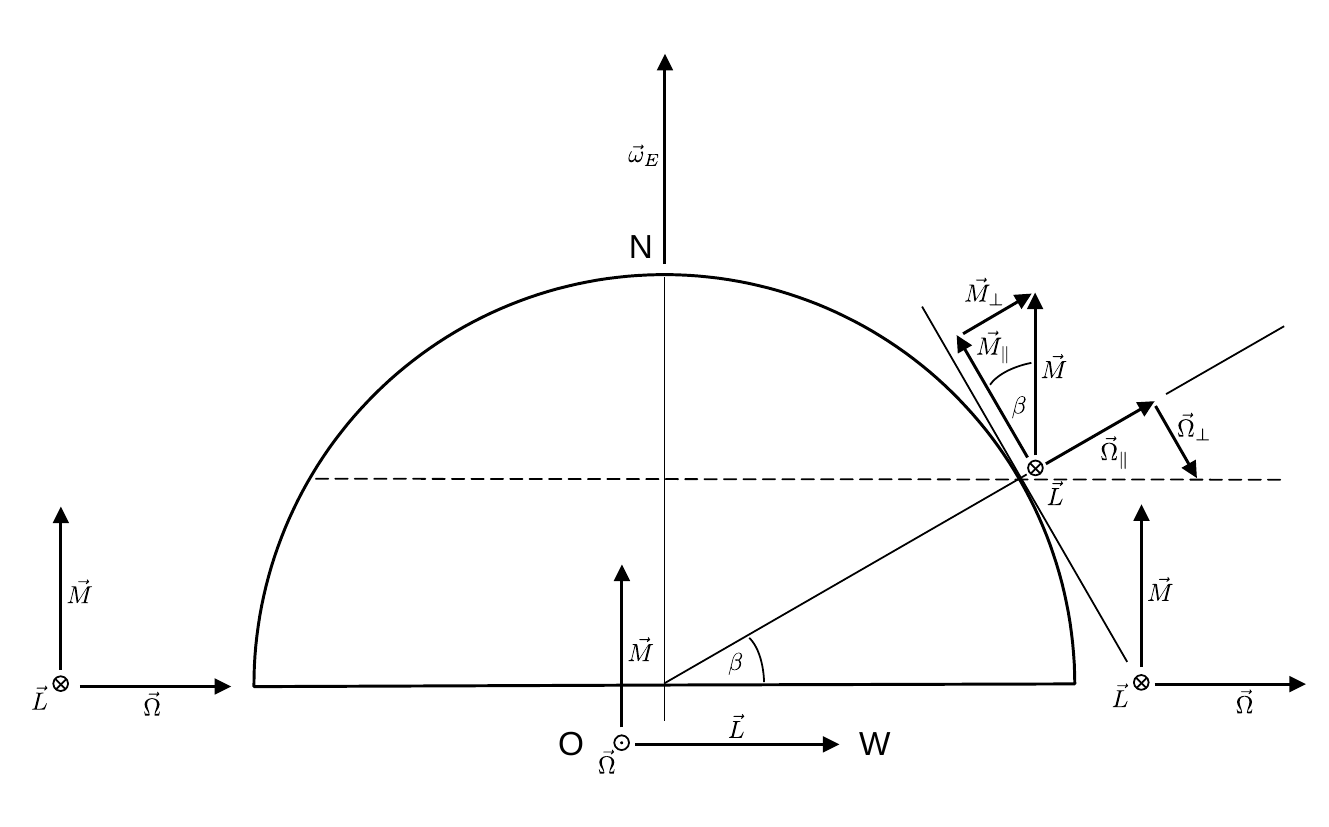
Skizze 7 (Geometrie zur Disksussion des Kreiselkompasses)
Die folgende Diskussion erfordert wie wiederholte Anwendung der "Rechten-Hand-Regel" zur Auswertung der Richtung des Kreuzprodukts aus Gleichung (3).
Die Erde dreht sich mit der Winkelgeschwindigkeit \vec\omega_{E}. Ein Kreiselkompass, der auf Höhe des Äquators, in Ost-West-Richtung ausgerichtet ist erfährt durch die Drehung der Erde das Drehmoment \vec{M}. Dies führt zur Präzession mit der Winkelgeschwindigkeit \vec{\Omega}, die die Figurenachse des Kreisels in Nord-Süd-Richtung (\vec{L} im Bild nach oben) und damit parallel zu \vec\omega_{E} ausrichtet. Dieser Umstand ist in Skizze 7, in drei Positionen entlang des Äquators, in den unteren drei Achsenkreuzen aus \vec{\Omega}, \vec{L} und \vec{M} dargestellt.
Für die weiteren Betrachtungen ist zu berücksichtigen, dass sich der Kreisel in der jeweiligen Tangentialebene auf der Halbkugel nur in horizontaler Richtung bewegen kann, während er in vertikaler Richtung, durch die Schraubenfedern, gebunden ist. Wäre der Kreisel nicht in vertikaler Richtung gebunden, würde sich \vec{L} im Bild wiederum nach oben und damit damit parallel zu \vec\omega_{E} ausrichten. Durch die Bindung ist es erforderlich \vec{M} in zwei Komponenten \vec M_{\parallel} (horizontal) und \vec M_{\perp} (vertikal) in der Tangentialebene auf der Halbkugel zu zerlegen. Der Anteil \vec M_{\parallel} führt zur Präzession mit \vec\Omega_{\parallel}, die wiederum dazu führt, dass sich der Kreisel innerhalb der Horizontalen in Nord-Süd-Richtung ausrichtet. Im Bild richtet sich \vec{L} nach oben links weisend aus. Der Anteil \vec M_{\perp} würde zur Präzession mit der Winkelgeschwindigkeit \vec\Omega_{\perp} führen, die den Kreisel aus der Horizontalen in die Vertikale (im Bild richtet sich \vec{L} nach oben rechts weisend aus) ausrichten würde. Dieser Anteil der Präzession ist durch die Bindung an den entsprechenden Kardanrahmen jedoch unterbunden. Im Vergleich zum Äquator ist der Effekt der Präzession um den Faktor \cos\beta reduziert.
Am Nordpol findet keine Einstellung des Kreisels in Nord-Süd-Richtung statt. Der Kreisel würde sich senkrecht in die Vertikale drehen. Diese Drehung ist jedoch durch die Bindung an den Kardanrahmen unterbunden.