-
- Downloads
Including a better resolution of the differences between the used measurement...
Including a better resolution of the differences between the used measurement methods, apart from that a few minor fixes
Showing
- Photoeffekt/doc/Hinweise-Photoeffekt.md 33 additions, 17 deletionsPhotoeffekt/doc/Hinweise-Photoeffekt.md
- Photoeffekt/doc/Hinweise-Versuchsdurchfuehrung-a.md 5 additions, 5 deletionsPhotoeffekt/doc/Hinweise-Versuchsdurchfuehrung-a.md
- Photoeffekt/doc/Hinweise-Versuchsdurchfuehrung.md 7 additions, 7 deletionsPhotoeffekt/doc/Hinweise-Versuchsdurchfuehrung.md
- Photoeffekt/figures/PhotoeffektSkizze.odg 0 additions, 0 deletionsPhotoeffekt/figures/PhotoeffektSkizze.odg
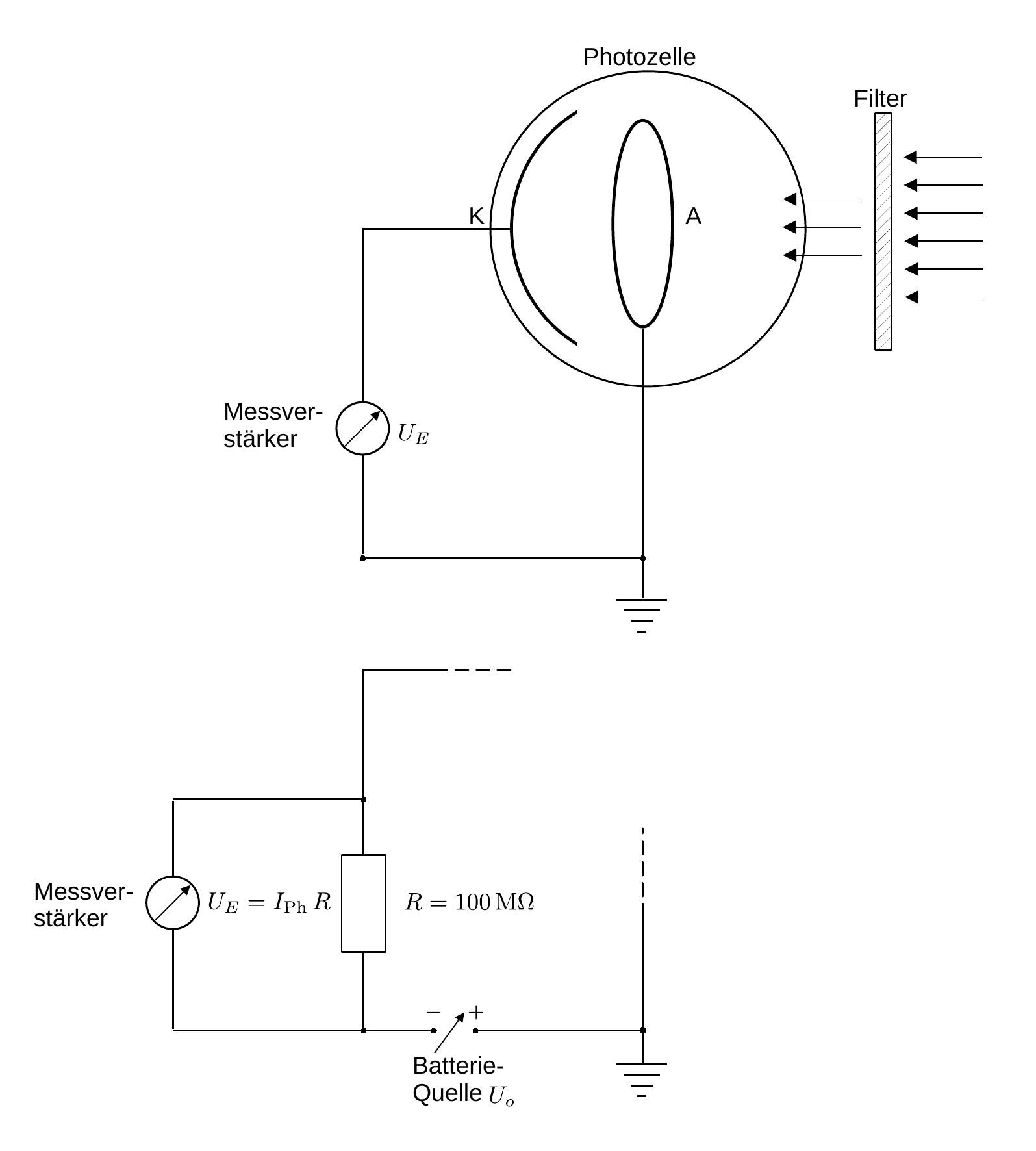
- Photoeffekt/figures/PhotoeffektSkizze.png 0 additions, 0 deletionsPhotoeffekt/figures/PhotoeffektSkizze.png
No preview for this file type
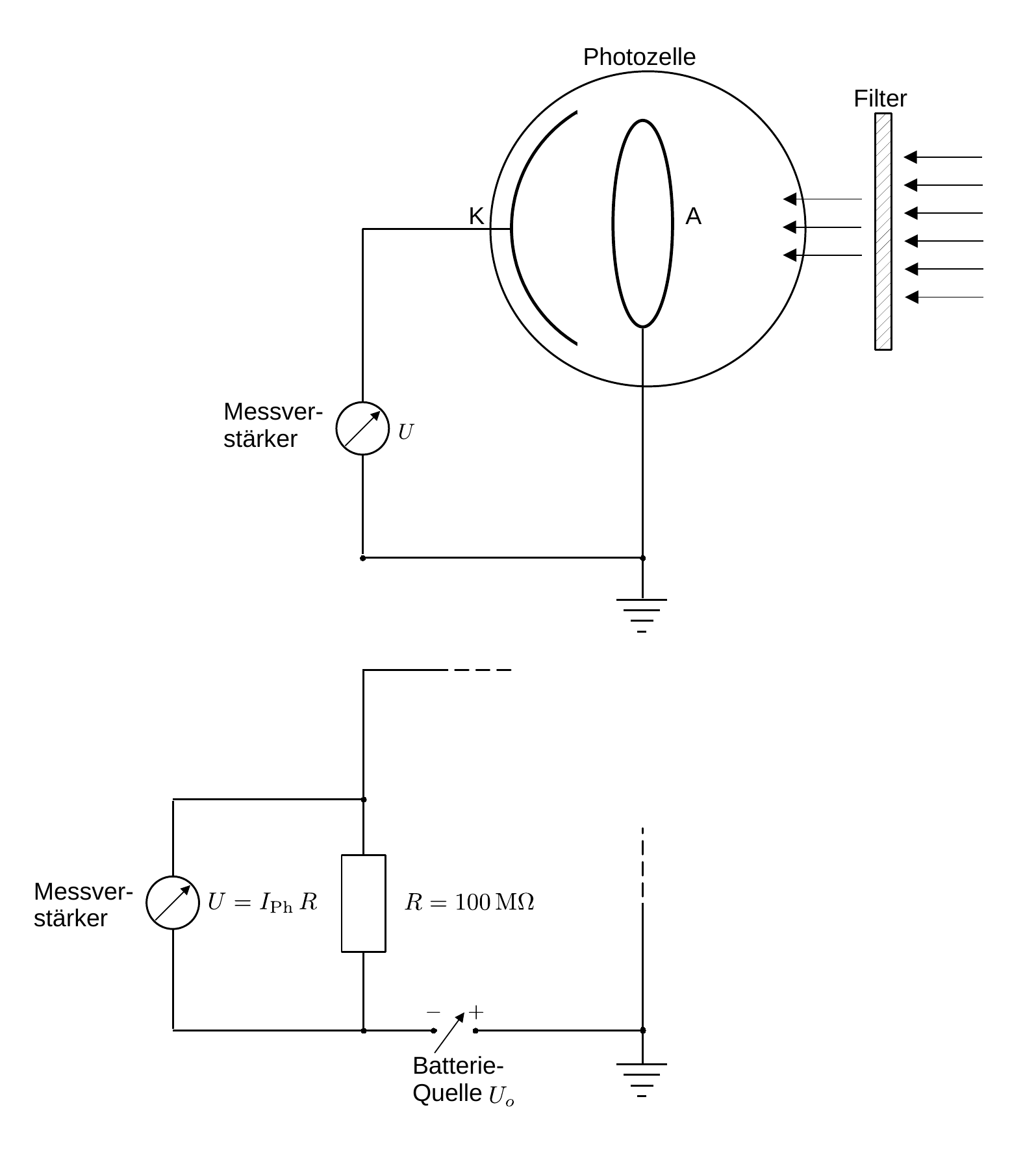
| W: | H:
| W: | H: