Hinweise-Hysterese.md



Hinweise für den Versuch Ferromagnetische Hysterese

Magnetisierung und Polarisation
In einem Ferromagneten liegen mikroskopische magnetische Dipole (Elementarmagnete) vor. Richten sich diese über größere makroskopische Bereiche (die sog. Weiss-Bezirke) hinweg gleich aus, bildet der Ferromagnet ein makroskopisches magnetisches Dipolmoment 
 $\vec{m}$ 
 aus und wird (permanent) magnetisch.
Die Größe
 $\begin{equation*} \vec{M}=\frac{\mathrm{d}\vec{m}}{\mathrm{d}V} \end{equation*}$ 
bezeichnet man als Magnetisierung.
Die Größe

\begin{equation*}
\vec{J}=\mu_{0}\vec{M}
\end{equation*}

bezeichnet man als magnetische Polarisation.
Legt man an einen Ferromagneten ein äußeres magnetisches Feld an richten sich proportional zur Stärke des Feldes immer mehr Elementarmagnete aus wodurch 
\vec{M}
 steigt. Dieser Vorgang trägt selbst wieder zur Erhöhung des Magnetfelds bei.
Erwärmung des Ferromagneten erhöht dessen Entropie. Dies wirkt der Ausrichtung der Elementarmagnete entgegen und senkt 
\vec{M}
. Oberhalb der Curie-Temperatur T_{C}
 geht \vec{M}
 spontan ganz verloren. Für Eisen ist T_{C}=1033\ \mathrm{K}
.

Flussdichte und Feldstärke
Die Größe und Richtung eines magnetischen Feldes wird durch die magnetische Flussdichte 
\vec{B}
 (mit dem Betrag B=|\vec{B}|
) quantifiziert.
Legt man an einen Ferromagneten ein äußeres magnetisches Feld der Flussdichte 
\vec{B}_{0}
 an wird diese durch \vec{J} erhöht:

\begin{equation*}
\begin{split}
\vec{B} &= \vec{B}_{0} + \vec{J}.\\
\end{split}
\end{equation*}

Neben \vec{B}
 definiert man die magnetische Feldstärke

\begin{equation*}
\vec{H}\equiv\frac{1}{\mu_{0}}\left(\vec{B} - \vec{J}\right),
\end{equation*}

(mit dem Betrag H=|\vec{H}|
), die die Größe des magnetischen Feldes quantifiziert, das sich allein aus elektrischen Leitungs- und Verschiebungsströmen, jedoch nicht aus der zusätzlichen Polarisation magnetischer Materie ergibt. Den Quotienten

\begin{equation*}
\mu\equiv\frac{B}{H}
\end{equation*}

bezeichnet man als magnetische Permeabilität. Zwischen \vec{H}
 und \vec{M} besteht der Zusammenhang:

\begin{equation*}
\begin{split}
&\vec{B} = \mu_{0}\left(\vec{H}+\vec{M}\right) = \mu\,\vec{H};\\
&\\
&\vec{M} = \frac{\mu-\mu_{0}}{\mu_{0}}\vec{H} = \underbrace{\left(\frac{\mu}{\mu_{0}}-1\right)}\vec{H},\\
&\hphantom{ccccccccccccccccccccc}\equiv\chi\\
\end{split}
\end{equation*}

d.h. \vec{M}\propto\vec{H}
. Die Proportionalitätskonstante \chi
 ist eine physikalische Größe der Dimension Zahl und wird als magnetische Suszeptibilität bezeichnet. Die Größe

\begin{equation*}
\mu_{r}\equiv\frac{\mu}{\mu_{0}} = \chi+1
\end{equation*}

heisst relative Permeabilität. Für Ferro- und Ferritmagnete ist \mu_{r}
 nicht konstant, sondern von H
 abhängig.

Hysterese
Trägt man eine der Größen 
B,\ J=|\vec{J}|,\ \mu,\ \chi
 als Funktion von B_{0}
 oder H
 auf bezeichnet man dies als Magnetisierungs- oder Hysteresekurve. Ihr Verlauf hängt nicht nur vom Material und der Temperatur, sondern auch von der Verlaufsgeschichte der Messung ab. Diesen Umstand bezeichnet man als Hysterese. Eine typische Magnetisierungskurve eines Ferromagneten ist in Abbildung 1 gezeigt:


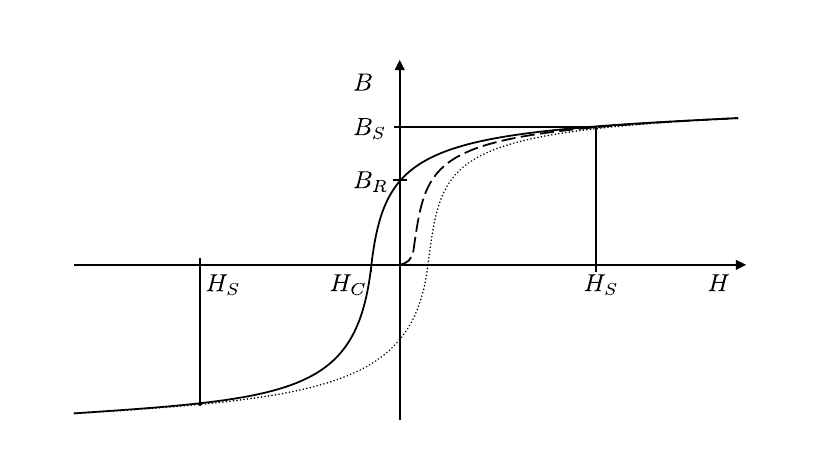
Abbildung 1: (Typischer Verlauf einer Magnetisierungskurve 
B(H)
 für einen Ferromagneten)


Die gestrichelte Linie stellt die Neukurve dar, bei der der nicht magnetische Ferromagnet zum ersten Mal durch ein äußeres Feld H
 magnetisiert wird.
Oberhalb einer maximalen Feldstärke H_{S}
 geht das Material in Sättigung, d.h. es richten sich keine weiteren Elementarmagnete mehr aus und B
 nimmt proportional zu H
 zu (\Delta B = \mu_{0}\Delta H
). Der dazugehörige Wert für B
 ist in Abbildung 1 mit B_{S}
 gekennzeichnet.
Regelt man H
 wieder bis auf 0 zurück bleibt \vec{J}
 teilweise erhalten. Die Größe B_{R}=J_{R}
 bezeichnet man als Remanenz.
Um die Polarisation des Ferromagneten aufzuheben bedarf es eines nicht verschwindenden Gegenfelds mit der Stärke H_{C}
. Man bezeichnet H_{C}
 als Koerzitivfeldstärke.
Alternativ kann die Magnetisierung durch Erhitzen auf Temperaturen oberhalb T_{C}
, oder durch Wechselfeldbetrieb mit langsam bis auf 0 abnehmender Feldstärke H\to 0
 aufgehoben werden.

Variiert man nach Durchlaufen der Neukurve 
H
 zwischen den Werten \pm H_{0}
 und misst jeweils die Werte für B
 durchläuft man eine Hysterese- oder Magnetisierungsschleife, die das Wertepaar (H,B)=(0,0) nicht
mehr enthält. Schleifen zu kleineren Werten H<H_{0}
 liegen ganz innerhalb dieser Schleife.
Das Integral

\begin{equation*}
w\equiv\oint B\,\mathrm{d}H = \frac{W}{V}
\end{equation*}

hat die Dimension [\text{Arbeit/Volumen}]
 und beschreibt die Arbeit pro Volumeneinheit, die während eines Magnetisierungszyklus aufgewendet werden muss, um den Spulenkern mit dem Volumen V
 um zu magnetisieren. Bei Anliegen einer sinusförmigen Wechselspannung der Frequenz \nu entspricht das Produkt

\begin{equation}
P_{\mathrm{hyst}}\equiv w\,\nu\,V
\end{equation}

der Verlustleistung durch Ummagnetisierung, die auch als Hystereseverlust bezeichnet wird.

Methode zur Messung des Hystereseverlusts
Zur Messung des Hystereseverlusts verfolgen wir die folgende Strategie:

Oszilloskopische Darstellung der Magnetisierungsschleife B(H)
.
Elektronische Auslese, Kalibration der Achsen, Glätten der Kurve und numerische Integration der eingeschlossenen Fläche.
Bestimmung von P_{\mathrm{hsyt}}
 nach Gleichung (1).

Ein entsprechendes Schaltbild zur Darstellung der Hysteresschleife auf dem Oszilloskop ist in Abbildung 2 gezeigt:


Abbildung 2: (Schaltbild zur oszilloskopischen Aufzeichnung einer Magnetisierungskurve 
B(H)
)

Die Primärspule mit 
N_{1}
 Windungen mit Eisenkern wird durch anbringen einer Sekundärspule mit N_{2} Windungen zum Transformator ergänzt. Im Primärkreis (links im Bild) wird

\begin{equation*}
U_{H}=I\,R_{1}
\end{equation*}

als Maß für den Strom auf CH1 des Oszilloskops eingelesen und im XY-Modus des Oszilloskops auf der x-Achse dargestellt. Durch den Eisenkern gilt selbst für die vorliegenden relativ kurzen Spulen

\begin{equation*}
H = N_{1}\,\frac{I}{\ell} = N_{1}\,\frac{U_{H}}{R_{1}\,\ell}.
\end{equation*}

Beachten Sie, dass \ell
 nicht der Länge der Spule sondern der Länge der Magnetfeldlinien im Eisenkern entspricht. Eine Erklärung hierzu finden Sie z.B. im Abschnitt Magnetfeld einer langen Spule in der Dokumentation für den Versuch Spezifische Ladung des Elektrons. Entsprechende Werte für die mittlere Länge der Feldlinien für die am Versuch vorliegenden Eisen- und Ferritkerne finden Sie im Datenblatt zum Versuch.
B wird durch Integration der in der Sekundärspule induzierten Spannung

\begin{equation*}
U_{i} = N_{2}\,A\,\dot{B}
\end{equation*}

gewonnen, wobei A
 der Fläche der Sekundärspule entspricht. Als physikalischer Integrator dient ein RC
-Integrierglied bestehend aus einem in Reihe geschalteten Widerstand R_{2}
 und einem Kondensator C
. Über den Kondensator wird U_{B}
 auf CH2 des Oszilloskops abgegriffen. (Zur Funktionsweise eines RC
-Integrierglieds siehe Aufgabe 1 des Versuchs Netzwerke und Leitungen.) Sind R_{2}
 und C so gewählt, dass die Bedingung

\begin{equation*}
R_{2}\gg\frac{1}{\omega\,C};\qquad \text{mit: }\omega=2\pi\,\nu
\end{equation*}

erfüllt ist gilt:

\begin{equation*}
U_{B} = \frac{1}{C\,R_{2}}\int U_{i}\,\mathrm{d}t = \frac{N_{2}\,A}{C\,R_{2}}\int \dot{B}\,\mathrm{d}t = \frac{N_{2}\,A}{C\,R_{2}}\,B.
\end{equation*}

U_{B}
 stellt die y
-Achse im XY-Modus des Oszilloskops dar. B ermittelt sich darus durch Umstellen:

\begin{equation*}
B = \frac{C\,R_{2}}{N_{2}\,A}\,U_{B}
\end{equation*}


Eisenverluste
Der Hystrereseverlust ist bei einem Material mit schmaler Magnetisierungsschlafe gering. Solche Materialen bezeichnet man als weichmagnetisch. Sie weisen i.a.

eine geringe Koerzitivfeldstärke;
hohe Remanenz und
große Leitfähigkeit auf.

Demgegenüberstehen hartmagnetische Werkstoffe, die i.a. eine hohe Koerzitivfeldstärke und hohe Remanenz aufweisen. Die Magnetisierungskurve solcher Werkstoffe ist im Idealfall rechteckig.
Für die den Hystereseverlust gilt näherungsweise die Formel

\begin{equation*}
P_{\mathrm{hyst}} \approx k_{H}\frac{4\,H_{C}}{\rho}\,B_{\mathrm{max}}\,\nu,
\end{equation*}

wobei k_{H}\approx1
 ein Formfaktor, \rho
 die Dichte des Kernmaterials, \nu
 die Frequenz der Ummagnetisierung und B_{\mathrm{max}}
 die maximal induzierte Flussdichte sind.
Ummagnetisierung ist nicht der einzige Mechanismus, durch den Energie bei der Magnetisierung von Ferromagneten verloren geht (siehe Eisenverluste). Gerade die hohe Leitfähigkeit weichmagnetischer Werkstoffe führt zum Energieverlust durch Wirbelströme. Diese unterbindet man, indem man den Eisenkern durch dünne Bleche ersetzt die wechselweise mit isolierendem Material lamelliert werden, wodurch der Widerstand entlang der Strecke

\begin{equation*}
\oint \vec{E}\cdot\mathrm{d}\vec{s}
\end{equation*}

im Eisenkern so weit wie möglich erhöht wird. Der Energieverlust durch Wirbelströme kann durch die folgende Formel beschrieben werden:

\begin{equation*}
P_{w} = \frac{\pi^{2}\sigma\,d^{2}}{6\rho}\,B_{\mathrm{max}}\,\nu,
\end{equation*}

wobei \sigma
 der Leitfähigkeit und d
 die Dicke des Blechs sind.
Alternativ wird Eisen pulverisiert und in isolierendem Material in seine endgültige Form gepresst. Die verlorene Energie wird in Wärme umgewandelt. Im Versuch können Sie diese Erfahrung leicht machen, indem Sie einen lamellierten durch einen Volleisenkern ersetzen.

Essentials
Was Sie ab jetzt wissen sollten:

Den Zusammenhang zwischen \vec{B},\ \vec{J},\,\vec{M}
 und \vec{H}
.
Die Bedeutung von \vec{H}
.
Das Aussehen und Zustandekommen einer Magnetisierungsschleife, sowie die Bedeutung von Koerzitivfeldsträrke und Remanenz.


Testfragen

Wie würde sich Abbildung 1 ändern, wenn man statt B
 die Polarisation J
 auf der y
-Achse auftragen würde.
Wie kann man aus Abbildung 1 ganz offensichtlich sehen, dass für Ferromagnete \mu
 von H
 abhängt?
Wie kann man aus Abbildung 1 ganz offensichtlich sehen, dass B
 von der Verlaufsgeschichte der Messung abhängt?


Navigation
Main