-
- Downloads
completion up to Exercise 2
Showing
- Schaltlogik/doc/Hinweise-Logik.md 138 additions, 2 deletionsSchaltlogik/doc/Hinweise-Logik.md
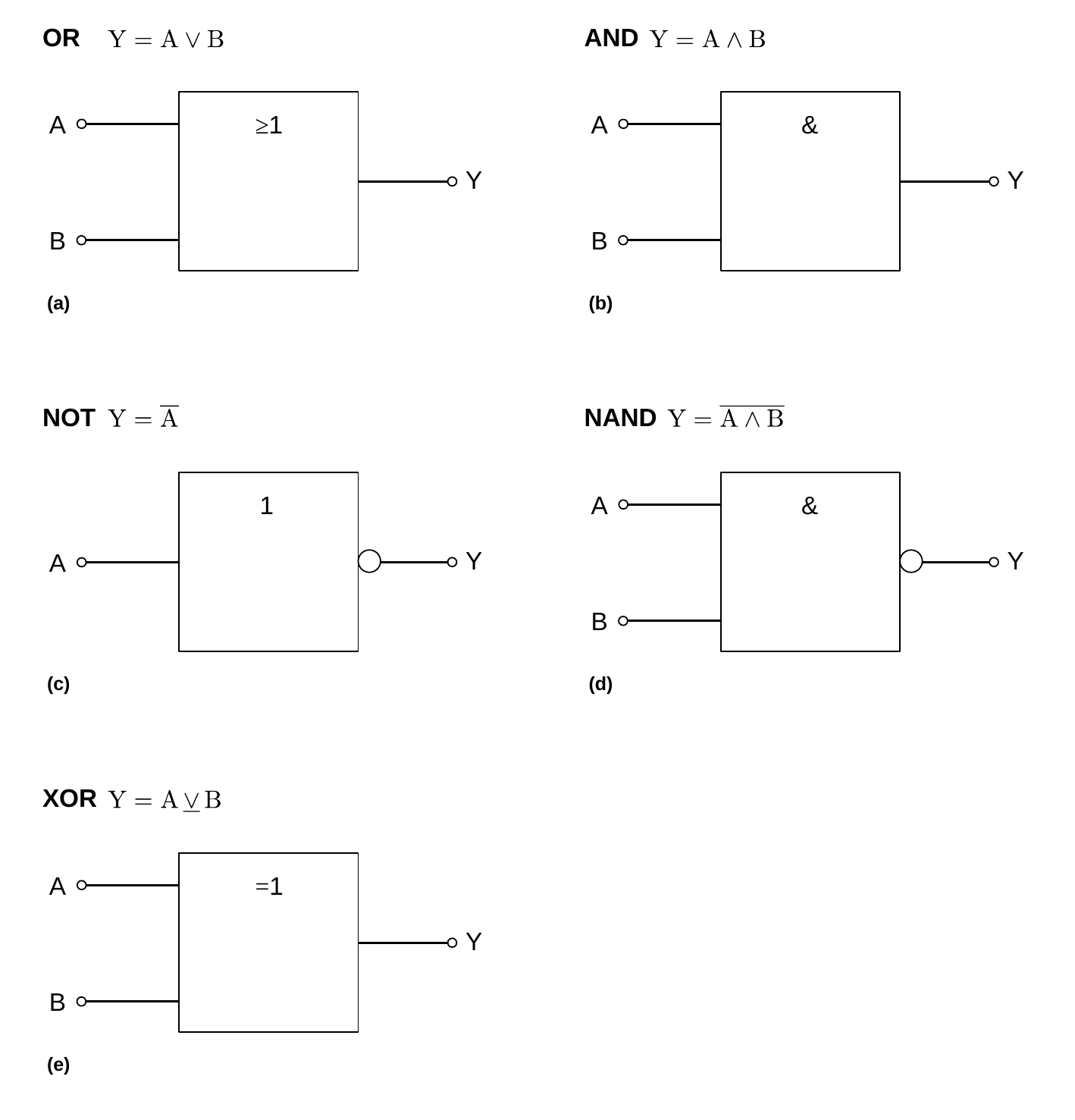
- Schaltlogik/figures/Symbole-Gatter.odg 0 additions, 0 deletionsSchaltlogik/figures/Symbole-Gatter.odg
- Schaltlogik/figures/Symbole-Gatter.png 0 additions, 0 deletionsSchaltlogik/figures/Symbole-Gatter.png
No preview for this file type

| W: | H:
| W: | H: